
Question Number 210392 by peter frank last updated on 08/Aug/24

Commented by mr W last updated on 09/Aug/24
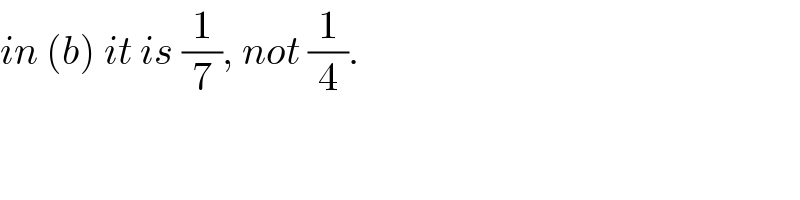
$${in}\:\left({b}\right)\:{it}\:{is}\:\frac{\mathrm{1}}{\mathrm{7}},\:{not}\:\frac{\mathrm{1}}{\mathrm{4}}. \\ $$
Answered by mr W last updated on 08/Aug/24
Commented by mr W last updated on 09/Aug/24

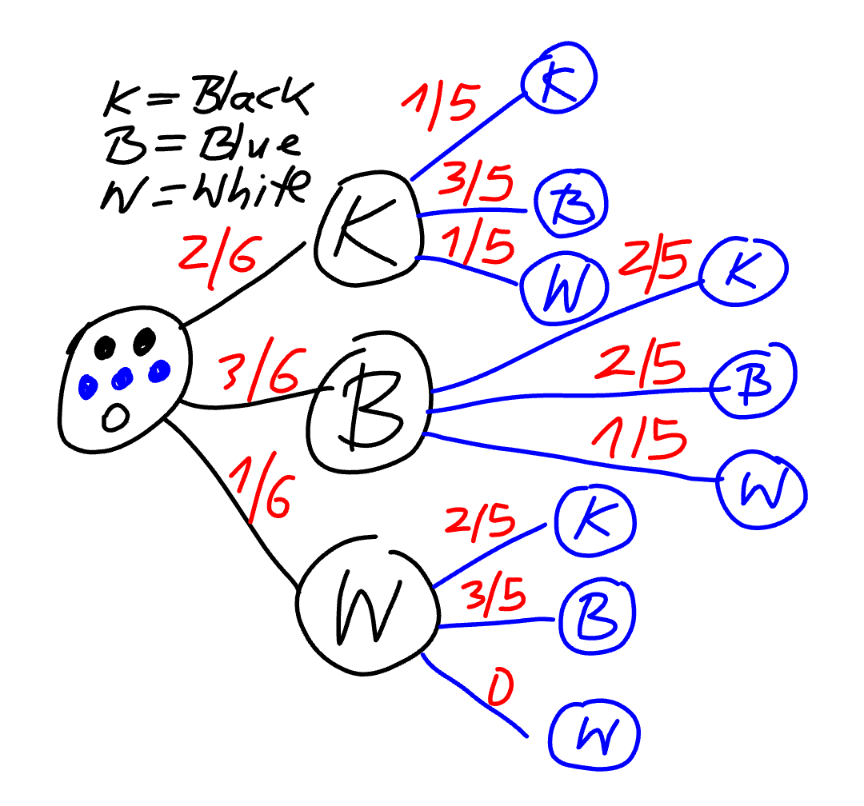
$$\left(\mathrm{1}\right) \\ $$$${p}=\frac{\mathrm{2}}{\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{15}} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$${n}={number}\:{of}\:{black}\:{marbles}\:{in}\:{jar} \\ $$$${p}=\frac{{n}}{{n}+\mathrm{4}}×\frac{{n}−\mathrm{1}}{{n}+\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\mathrm{3}{n}^{\mathrm{2}} −\mathrm{7}{n}−\mathrm{6}=\mathrm{0}\:\Rightarrow{n}=\mathrm{3} \\ $$$$\Rightarrow{one}\:{black}\:{marble}\:{must}\:{be}\:{added}\:{to} \\ $$$${the}\:{jar}. \\ $$$$ \\ $$$$\left(\mathrm{3}\right) \\ $$$${n}={number}\:{of}\:{blue}\:{marbles}\:{in}\:{jar} \\ $$$${p}=\frac{\mathrm{2}}{{n}+\mathrm{3}}×\frac{\mathrm{1}}{{n}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${n}^{\mathrm{2}} +\mathrm{5}{n}=\mathrm{0}\:\Rightarrow{n}=\mathrm{0} \\ $$$$\Rightarrow{all}\:\mathrm{3}\:{blue}\:{marbles}\:{must}\:{be}\:{removed} \\ $$$${from}\:{the}\:{jar}. \\ $$
Commented by peter frank last updated on 09/Aug/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
