
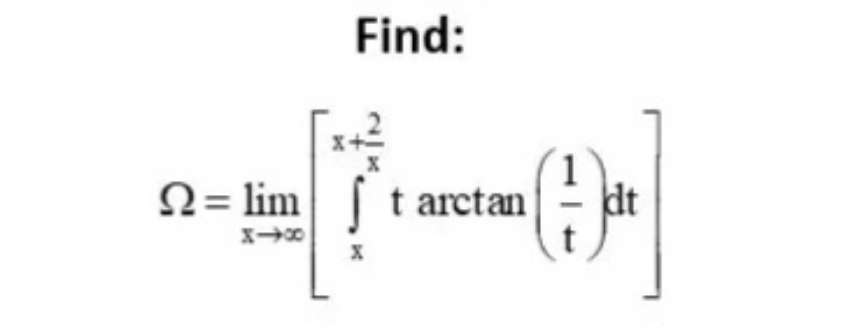
Question Number 210390 by hardmath last updated on 08/Aug/24
Answered by Berbere last updated on 08/Aug/24
![ttan^(−1) ((1/t))=f(t) lim_(x→∞) f(x)=1⇒∃M∈R_+ ∀x≥M (1/2) ≤f(x)≤(3/2) ⇒∀x≥M f(x)>0⇒F(x)=∫_M ^x f(x)dx is increase positive function ∀x≥M ⇒∫_x ^(x+(2/x)) ttan^(−1) ((1/t))dt=F(x+(2/x))−F(x) mean value Theorem ∃c∈]x,x+(2/x)[ suche x+(2/x)>c>x F(x+(2/x))−F(x)=(x+(2/x)−x)f(c)=(2/x)f(c) f is bounded lim_(x→∞) f(x)=1⇒lim_(x→0) F(x+(2/x))−F(x)=0](Q210404.png)
$${t}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}\right)={f}\left({t}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}\Rightarrow\exists{M}\in\mathbb{R}_{+} \:\forall{x}\geqslant{M}\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant{f}\left({x}\right)\leqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\forall{x}\geqslant{M} \\ $$$${f}\left({x}\right)>\mathrm{0}\Rightarrow{F}\left({x}\right)=\int_{{M}} ^{{x}} {f}\left({x}\right){dx}\:\:{is}\:{increase}\:{positive}\:{function}\:\forall{x}\geqslant{M} \\ $$$$\Rightarrow\int_{{x}} ^{{x}+\frac{\mathrm{2}}{{x}}} {t}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}\right){dt}={F}\left({x}+\frac{\mathrm{2}}{{x}}\right)−{F}\left({x}\right) \\ $$$$\left.{mean}\:{value}\:{Theorem}\:\exists{c}\in\right]{x},{x}+\frac{\mathrm{2}}{{x}}\left[\:{suche}\right. \\ $$$${x}+\frac{\mathrm{2}}{{x}}>{c}>{x} \\ $$$${F}\left({x}+\frac{\mathrm{2}}{{x}}\right)−{F}\left({x}\right)=\left({x}+\frac{\mathrm{2}}{{x}}−{x}\right){f}\left({c}\right)=\frac{\mathrm{2}}{{x}}{f}\left({c}\right) \\ $$$${f}\:{is}\:{bounded}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{F}\left({x}+\frac{\mathrm{2}}{{x}}\right)−{F}\left({x}\right)=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by hardmath last updated on 08/Aug/24
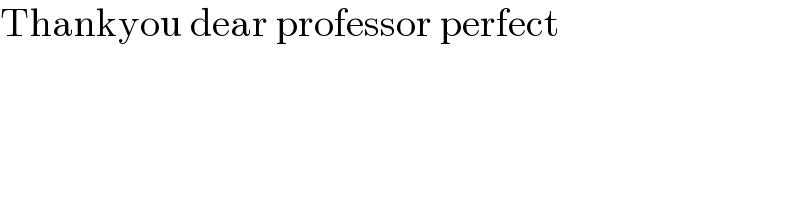
$$\mathrm{Thankyou}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{perfect} \\ $$
