Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 210375 by Spillover last updated on 08/Aug/24

Commented by som(math1967) last updated on 08/Aug/24

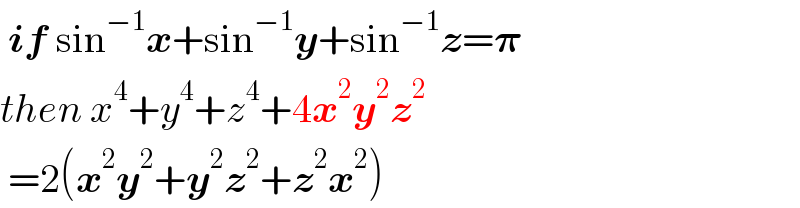
if sin^(−1) x+sin^(−1) y+sin^(−1) z=𝛑 then x^4 +y^4 +z^4 +4x^2 y^2 z^2 =2(x^2 y^2 +y^2 z^2 +z^2 x^2 )

$$\:\boldsymbol{{if}}\:\mathrm{sin}^{−\mathrm{1}} \boldsymbol{{x}}+\mathrm{sin}^{−\mathrm{1}} \boldsymbol{{y}}+\mathrm{sin}^{−\mathrm{1}} \boldsymbol{{z}}=\boldsymbol{\pi} \\ $$$${then}\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} +\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} \boldsymbol{{z}}^{\mathrm{2}} \\ $$$$\:=\mathrm{2}\left(\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \boldsymbol{{z}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} \boldsymbol{{x}}^{\mathrm{2}} \right) \\ $$

Commented by som(math1967) last updated on 08/Aug/24

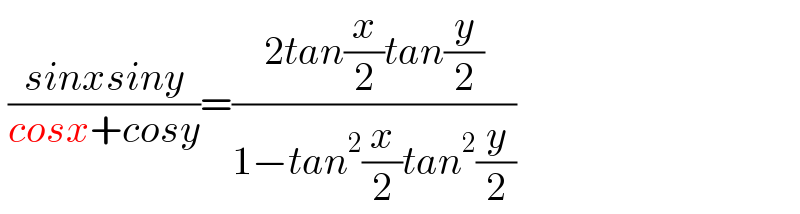
((sinxsiny)/(cosx+cosy))=((2tan(x/2)tan(y/2))/(1−tan^2 (x/2)tan^2 (y/2)))

$$\:\frac{{sinxsiny}}{{cosx}+{cosy}}=\frac{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}{tan}\frac{{y}}{\mathrm{2}}}{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{tan}^{\mathrm{2}} \frac{{y}}{\mathrm{2}}} \\ $$

Commented by Spillover last updated on 08/Aug/24

correct.thank you

$${correct}.{thank}\:{you} \\ $$

Commented by Spillover last updated on 08/Aug/24

correct.thank you

$${correct}.{thank}\:{you} \\ $$

Answered by som(math1967) last updated on 08/Aug/24

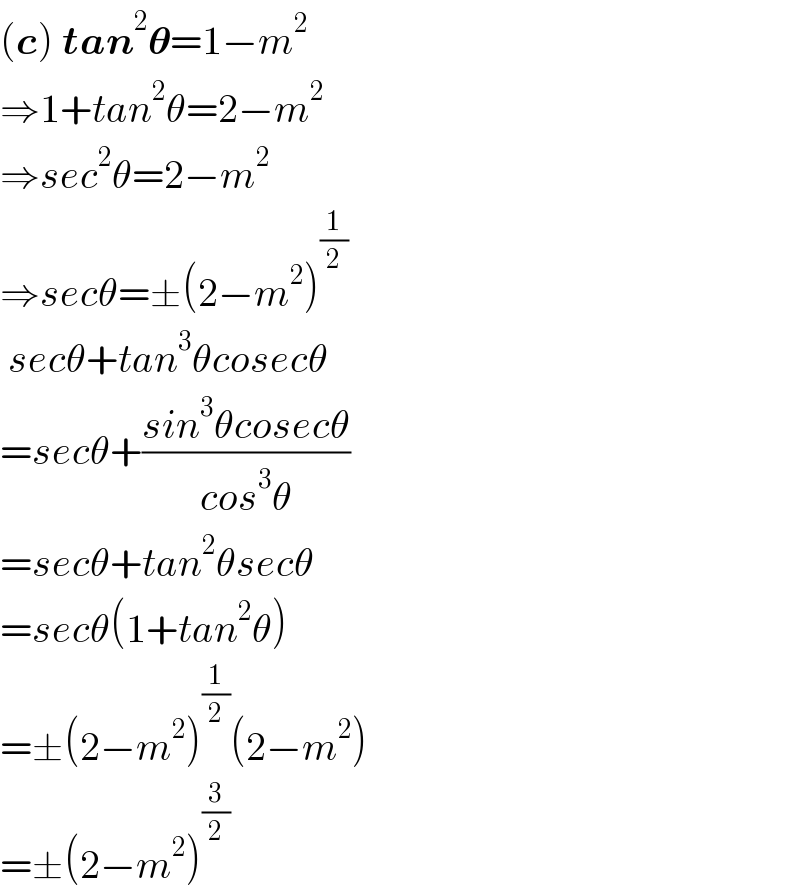
(c) tan^2 𝛉=1−m^2 ⇒1+tan^2 θ=2−m^2 ⇒sec^2 θ=2−m^2 ⇒secθ=±(2−m^2 )^(1/2) secθ+tan^3 θcosecθ =secθ+((sin^3 θcosecθ)/(cos^3 θ)) =secθ+tan^2 θsecθ =secθ(1+tan^2 θ) =±(2−m^2 )^(1/2) (2−m^2 ) =±(2−m^2 )^(3/2)

$$\left(\boldsymbol{{c}}\right)\:\boldsymbol{{tan}}^{\mathrm{2}} \boldsymbol{\theta}=\mathrm{1}−{m}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}+{tan}^{\mathrm{2}} \theta=\mathrm{2}−{m}^{\mathrm{2}} \\ $$$$\Rightarrow{sec}^{\mathrm{2}} \theta=\mathrm{2}−{m}^{\mathrm{2}} \\ $$$$\Rightarrow{sec}\theta=\pm\left(\mathrm{2}−{m}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:{sec}\theta+{tan}^{\mathrm{3}} \theta{cosec}\theta \\ $$$$={sec}\theta+\frac{{sin}^{\mathrm{3}} \theta{cosec}\theta}{{cos}^{\mathrm{3}} \theta} \\ $$$$={sec}\theta+{tan}^{\mathrm{2}} \theta{sec}\theta \\ $$$$={sec}\theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right) \\ $$$$=\pm\left(\mathrm{2}−{m}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{2}−{m}^{\mathrm{2}} \right) \\ $$$$=\pm\left(\mathrm{2}−{m}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$

Commented by Spillover last updated on 08/Aug/24

great.thanks

$${great}.{thanks} \\ $$

Answered by som(math1967) last updated on 08/Aug/24

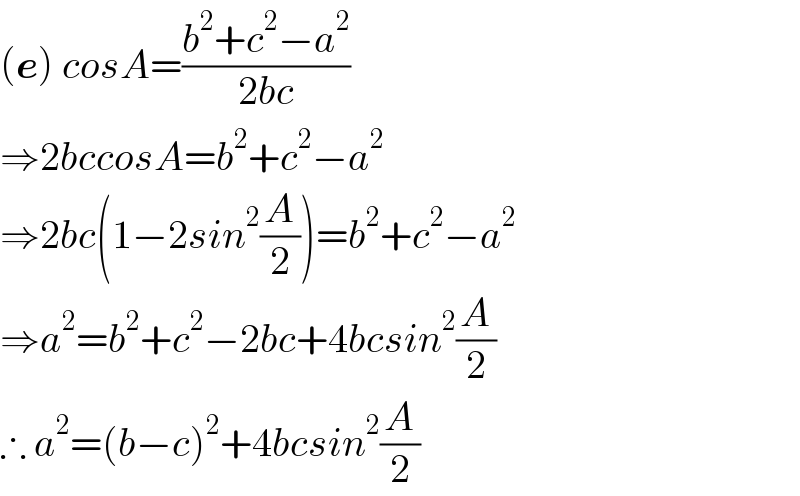
(e) cosA=((b^2 +c^2 −a^2 )/(2bc)) ⇒2bccosA=b^2 +c^2 −a^2 ⇒2bc(1−2sin^2 (A/2))=b^2 +c^2 −a^2 ⇒a^2 =b^2 +c^2 −2bc+4bcsin^2 (A/2) ∴ a^2 =(b−c)^2 +4bcsin^2 (A/2)

$$\left(\boldsymbol{{e}}\right)\:{cosA}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$$\Rightarrow\mathrm{2}{bccosA}={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{bc}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}\right)={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}+\mathrm{4}{bcsin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}} \\ $$$$\therefore\:{a}^{\mathrm{2}} =\left({b}−{c}\right)^{\mathrm{2}} +\mathrm{4}{bcsin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}} \\ $$

Commented by Spillover last updated on 08/Aug/24

great.thanks

$${great}.{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com