
Question Number 210374 by Spillover last updated on 08/Aug/24
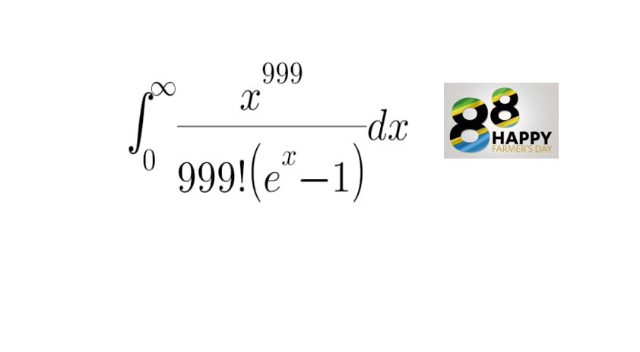
Commented by Frix last updated on 08/Aug/24

$$=\mathrm{Li}_{\mathrm{1000}} \:\left(\mathrm{1}\right) \\ $$$$\mathrm{Better}\:\mathrm{question}: \\ $$$$\mathrm{Show}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}}{{n}!}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{x}^{{n}} }{\mathrm{e}^{{x}} −\mathrm{1}}=\mathrm{Li}_{{n}+\mathrm{1}} \:\left(\mathrm{1}\right) \\ $$
Answered by Berbere last updated on 08/Aug/24
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{s}−\mathrm{1}} }{{e}^{{x}} −\mathrm{1}}{dx}=\zeta\left({s}\right)\Gamma\left({s}\right)\:\forall{S}\in\mathbb{C}\:{Re}\left({s}\right)>\mathrm{1} \\ $$
Commented by Spillover last updated on 09/Aug/24

$${great}. \\ $$
Answered by Spillover last updated on 09/Aug/24

Answered by Spillover last updated on 09/Aug/24

Answered by Spillover last updated on 09/Aug/24

