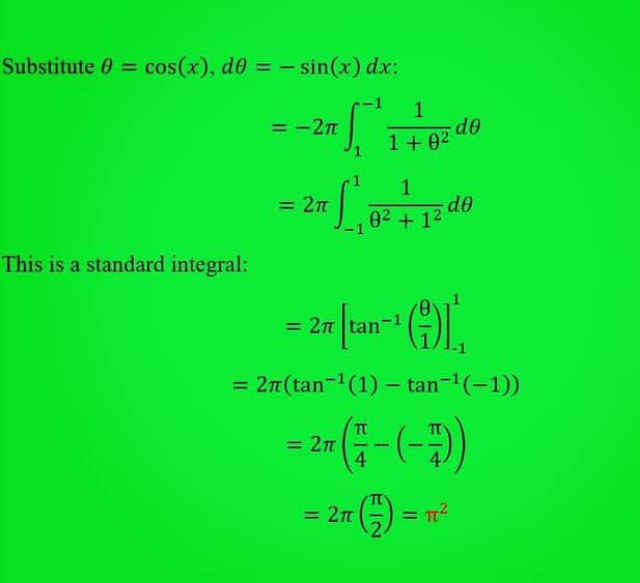Question Number 210372 by Spillover last updated on 08/Aug/24
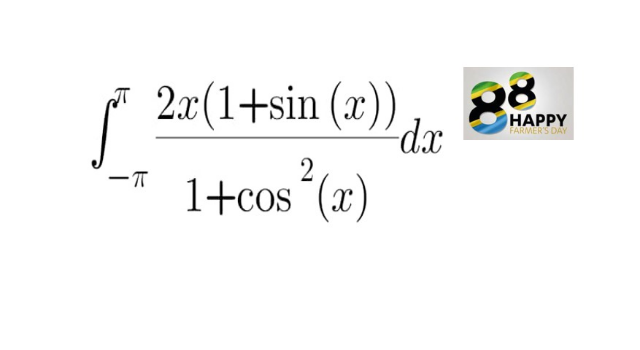
Commented by Frix last updated on 08/Aug/24

$$\mathrm{I}\:\mathrm{get}\:\pi^{\mathrm{2}} \\ $$
Answered by Berbere last updated on 08/Aug/24
![∫_(−π) ^π ((2x)/(1+cos^2 (x)))dx=0 ∫_(−π) ^π ((2xsin(x))/(1+cos^2 (x)))=[−2xtan^(−1) (cos(x))]_(−π) ^π +2∫_(−π) ^π tan^(−1) (cos(x))dx_(=0) tan^(−1) (cos(−x))dx=tan^(−1) (cos(x) ∗ =π^2](Q210405.png)
$$\int_{−\pi} ^{\pi} \frac{\mathrm{2}{x}}{\mathrm{1}+{cos}^{\mathrm{2}} \left({x}\right)}{dx}=\mathrm{0} \\ $$$$\int_{−\pi} ^{\pi} \frac{\mathrm{2}{xsin}\left({x}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({x}\right)}=\left[−\mathrm{2}{x}\mathrm{tan}^{−\mathrm{1}} \left({cos}\left({x}\right)\right)\right]_{−\pi} ^{\pi} +\mathrm{2}\int_{−\pi} ^{\pi} \mathrm{tan}^{−\mathrm{1}} \left({cos}\left({x}\right)\right){dx}_{=\mathrm{0}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left({cos}\left(−{x}\right)\right){dx}=\mathrm{tan}^{−\mathrm{1}} \left({cos}\left({x}\right)\:\:\ast\right. \\ $$$$=\pi^{\mathrm{2}} \\ $$
Answered by klipto last updated on 09/Aug/24
![using even and odd function ∫_(−𝛑) ^𝛑 ((2x+2xsin(x))/(1+cos^2 x)) ∫_(−𝛑) ^𝛑 ((2x)/(1+cos^2 x))dx+∫_(−𝛑) ^𝛑 ((2xsin(x))/(1+cos^2 x))dx ∫_(−𝛑) ^𝛑 ((2x)/(1+cos^2 x))=0[because f(−x)=−f(x)] ∫_(−𝛑) ^𝛑 ((2xsin(x))/(1+cos^2 x))dx=2∫_(−𝛑) ^𝛑 x•((sin(x))/(1+cos^2 x)) 2∫udv=uv−∫_(−𝛑) ^𝛑 vdu ∫_(−𝛑) ^𝛑 2x•((sin(x))/(1+cos^2 x))=−2xarctan(cosx)]_(−𝛑) ^𝛑 +2∫_(−𝛑) ^𝛑 arctan(cos(x)) ∫_(−𝛑) ^𝛑 2x•((sin(x))/(1+cos^2 x))=2[−xarctan(cos(x))]_(−𝛑) ^𝛑 +2∫_(−𝛑) ^𝛑 arctan(cos(x)) 2∫_(−𝛑) ^𝛑 2x•((sin(x))/(1+cos^2 x))=2[−𝛑tan^(−1) (cos(𝛑)−(−𝛑arctan(cos(−𝛑))]+0 =2[(𝛑^2 /4)+(𝛑^2 /4)]=((2𝛑^2 )/2)=𝛑^2 klipto−quanta.](Q210442.png)
$$ \\ $$$$\boldsymbol{\mathrm{using}}\:\boldsymbol{\mathrm{even}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{odd}}\:\boldsymbol{\mathrm{function}} \\ $$$$\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \frac{\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{2}\boldsymbol{\mathrm{xsin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \\ $$$$\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \frac{\mathrm{2}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}+\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \frac{\mathrm{2}\boldsymbol{\mathrm{xsin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}} \\ $$$$\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \frac{\mathrm{2}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}=\mathrm{0}\left[\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{f}}\left(−\boldsymbol{\mathrm{x}}\right)=−\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\right] \\ $$$$\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \frac{\mathrm{2}\boldsymbol{\mathrm{xsin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}=\mathrm{2}\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \boldsymbol{\mathrm{x}}\bullet\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}} \\ $$$$\mathrm{2}\int\boldsymbol{\mathrm{udv}}=\boldsymbol{\mathrm{uv}}−\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \boldsymbol{\mathrm{vdu}} \\ $$$$\left.\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \mathrm{2}\boldsymbol{\mathrm{x}}\bullet\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}=−\mathrm{2}\boldsymbol{\mathrm{xarctan}}\left(\boldsymbol{\mathrm{cosx}}\right)\right]_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} +\mathrm{2}\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \boldsymbol{\mathrm{arctan}}\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right) \\ $$$$\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \mathrm{2}\boldsymbol{\mathrm{x}}\bullet\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}=\mathrm{2}\left[−\boldsymbol{\mathrm{xarctan}}\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right)\right]_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} +\mathrm{2}\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \boldsymbol{\mathrm{arctan}}\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right) \\ $$$$\mathrm{2}\int_{−\boldsymbol{\pi}} ^{\boldsymbol{\pi}} \mathrm{2}\boldsymbol{\mathrm{x}}\bullet\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}=\mathrm{2}\left[−\boldsymbol{\pi\mathrm{tan}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\pi}\right)−\left(−\boldsymbol{\pi\mathrm{arctan}}\left(\boldsymbol{\mathrm{cos}}\left(−\boldsymbol{\pi}\right)\right)\right]+\mathrm{0}\right.\right. \\ $$$$=\mathrm{2}\left[\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{4}}+\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{4}}\right]=\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{2}}=\boldsymbol{\pi}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{klipto}}−\boldsymbol{\mathrm{quanta}}. \\ $$
Answered by Spillover last updated on 09/Aug/24

Answered by Spillover last updated on 09/Aug/24

Answered by Spillover last updated on 09/Aug/24