
Question Number 210289 by Abdullahrussell last updated on 05/Aug/24
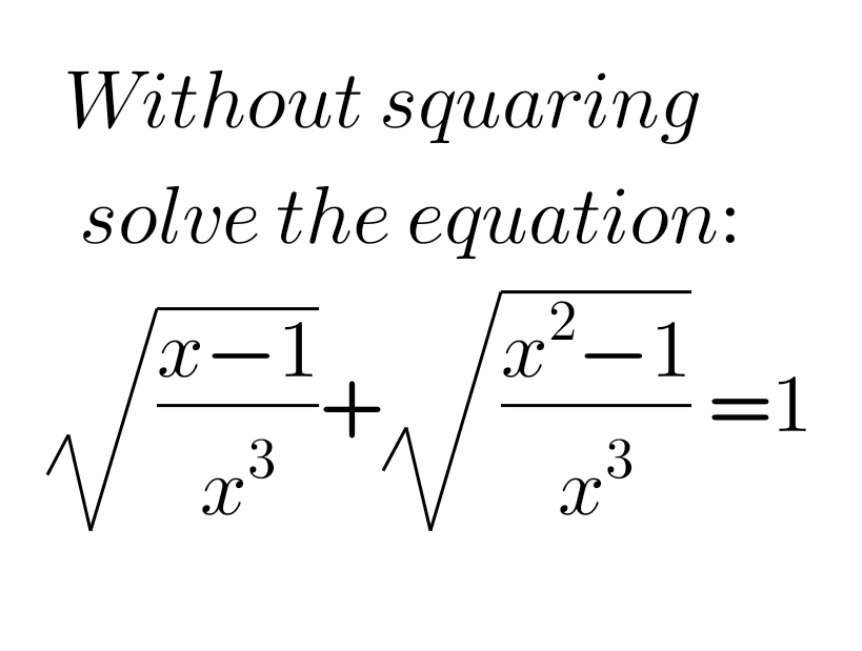
Answered by Frix last updated on 05/Aug/24
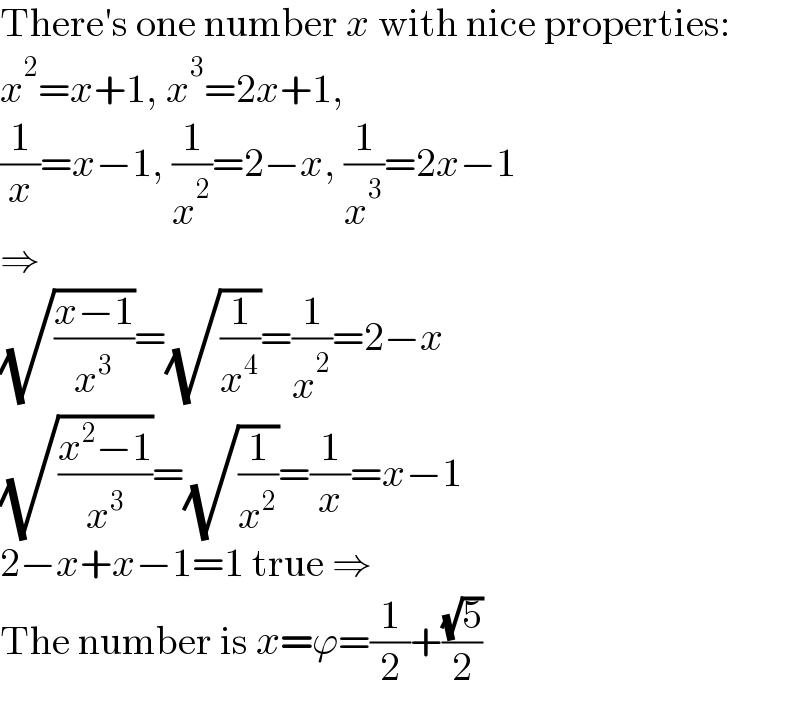
$$\mathrm{There}'\mathrm{s}\:\mathrm{one}\:\mathrm{number}\:{x}\:\mathrm{with}\:\mathrm{nice}\:\mathrm{properties}: \\ $$$${x}^{\mathrm{2}} ={x}+\mathrm{1},\:{x}^{\mathrm{3}} =\mathrm{2}{x}+\mathrm{1}, \\ $$$$\frac{\mathrm{1}}{{x}}={x}−\mathrm{1},\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{2}−{x},\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{2}{x}−\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\sqrt{\frac{{x}−\mathrm{1}}{{x}^{\mathrm{3}} }}=\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{2}−{x} \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{3}} }}=\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{{x}}={x}−\mathrm{1} \\ $$$$\mathrm{2}−{x}+{x}−\mathrm{1}=\mathrm{1}\:\mathrm{true}\:\Rightarrow \\ $$$$\mathrm{The}\:\mathrm{number}\:\mathrm{is}\:{x}=\varphi=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
