
Question Number 210248 by universe last updated on 04/Aug/24

Answered by mr W last updated on 04/Aug/24
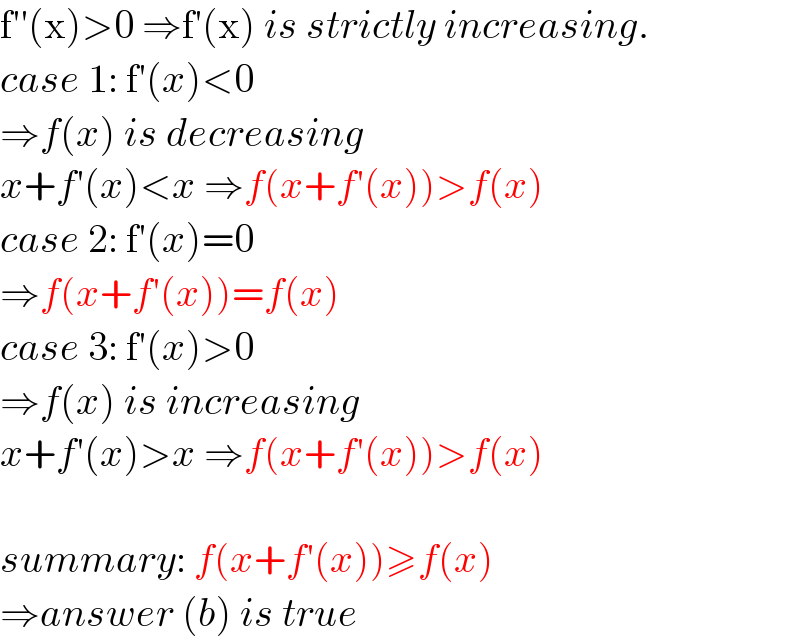
$$\mathrm{f}''\left(\mathrm{x}\right)>\mathrm{0}\:\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)\:{is}\:{strictly}\:{increasing}. \\ $$$${case}\:\mathrm{1}:\:\mathrm{f}'\left({x}\right)<\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{decreasing} \\ $$$${x}+{f}'\left({x}\right)<{x}\:\Rightarrow{f}\left({x}+{f}'\left({x}\right)\right)>{f}\left({x}\right) \\ $$$${case}\:\mathrm{2}:\:\mathrm{f}'\left({x}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}+{f}'\left({x}\right)\right)={f}\left({x}\right) \\ $$$${case}\:\mathrm{3}:\:\mathrm{f}'\left({x}\right)>\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{increasing} \\ $$$${x}+{f}'\left({x}\right)>{x}\:\Rightarrow{f}\left({x}+{f}'\left({x}\right)\right)>{f}\left({x}\right) \\ $$$$ \\ $$$${summary}:\:{f}\left({x}+{f}'\left({x}\right)\right)\geqslant{f}\left({x}\right) \\ $$$$\Rightarrow{answer}\:\left({b}\right)\:{is}\:{true} \\ $$
Commented by universe last updated on 04/Aug/24
$${thanl}\:{you}\:{so}\:{much}\:{sir} \\ $$
