Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 210235 by peter frank last updated on 03/Aug/24

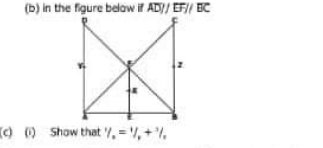
Commented by Pnk2024 last updated on 03/Aug/24

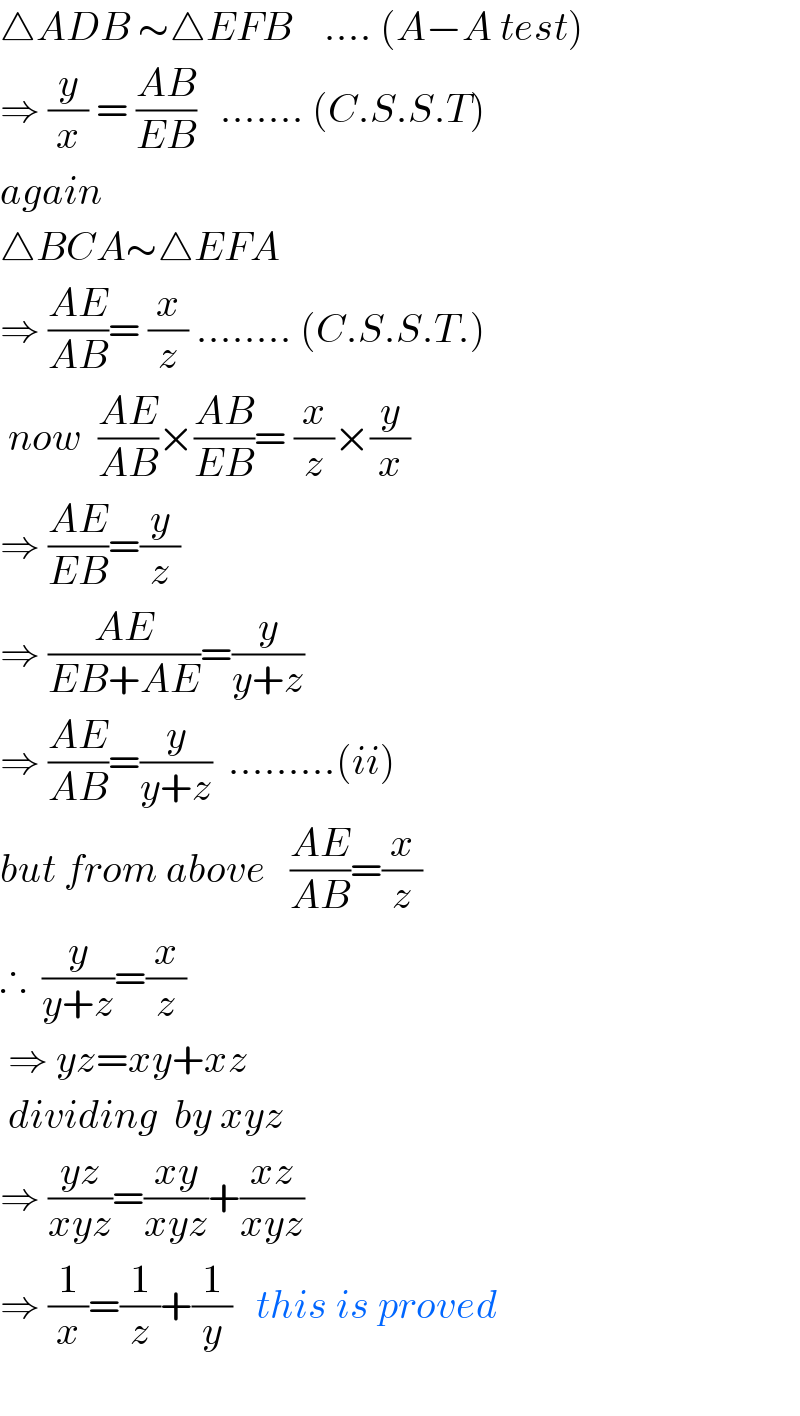
△ADB ∼△EFB .... (A−A test) ⇒ (y/x) = ((AB)/(EB)) ....... (C.S.S.T) again △BCA∼△EFA ⇒ ((AE)/(AB))= (x/z) ........ (C.S.S.T.) now ((AE)/(AB))×((AB)/(EB))= (x/z)×(y/x) ⇒ ((AE)/(EB))=(y/z) ⇒ ((AE)/(EB+AE))=(y/(y+z)) ⇒ ((AE)/(AB))=(y/(y+z)) .........(ii) but from above ((AE)/(AB))=(x/z) ∴ (y/(y+z))=(x/z) ⇒ yz=xy+xz dividing by xyz ⇒ ((yz)/(xyz))=((xy)/(xyz))+((xz)/(xyz)) ⇒ (1/x)=(1/z)+(1/y) this is proved

$$\bigtriangleup{ADB}\:\sim\bigtriangleup{EFB}\:\:\:\:....\:\left({A}−{A}\:{test}\right) \\ $$$$\Rightarrow\:\frac{{y}}{{x}}\:=\:\frac{{AB}}{{EB}}\:\:\:.......\:\left({C}.{S}.{S}.{T}\right) \\ $$$${again} \\ $$$$\bigtriangleup{BCA}\sim\bigtriangleup{EFA} \\ $$$$\Rightarrow\:\frac{{AE}}{{AB}}=\:\frac{{x}}{{z}}\:........\:\left({C}.{S}.{S}.{T}.\right) \\ $$$$\:{now}\:\:\frac{{AE}}{{AB}}×\frac{{AB}}{{EB}}=\:\frac{{x}}{{z}}×\frac{{y}}{{x}} \\ $$$$\Rightarrow\:\frac{{AE}}{{EB}}=\frac{{y}}{{z}} \\ $$$$\Rightarrow\:\frac{{AE}}{{EB}+{AE}}=\frac{{y}}{{y}+{z}} \\ $$$$\Rightarrow\:\frac{{AE}}{{AB}}=\frac{{y}}{{y}+{z}}\:\:.........\left({ii}\right) \\ $$$${but}\:{from}\:{above}\:\:\:\frac{{AE}}{{AB}}=\frac{{x}}{{z}} \\ $$$$\therefore\:\:\frac{{y}}{{y}+{z}}=\frac{{x}}{{z}}\:\: \\ $$$$\:\Rightarrow\:{yz}={xy}+{xz} \\ $$$$\:{dividing}\:\:{by}\:{xyz} \\ $$$$\Rightarrow\:\frac{{yz}}{{xyz}}=\frac{{xy}}{{xyz}}+\frac{{xz}}{{xyz}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{y}}\:\:\:{this}\:{is}\:{proved} \\ $$$$ \\ $$

Commented by peter frank last updated on 04/Aug/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by mr W last updated on 04/Aug/24

Commented by mr W last updated on 04/Aug/24

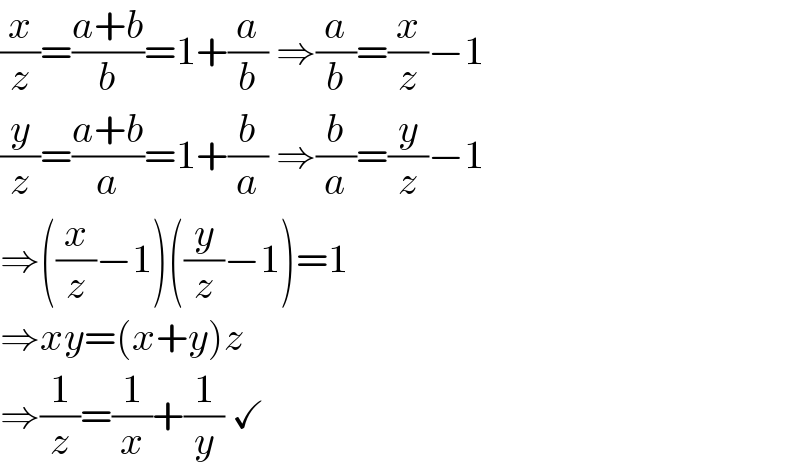
(x/z)=((a+b)/b)=1+(a/b) ⇒(a/b)=(x/z)−1 (y/z)=((a+b)/a)=1+(b/a) ⇒(b/a)=(y/z)−1 ⇒((x/z)−1)((y/z)−1)=1 ⇒xy=(x+y)z ⇒(1/z)=(1/x)+(1/y) ✓

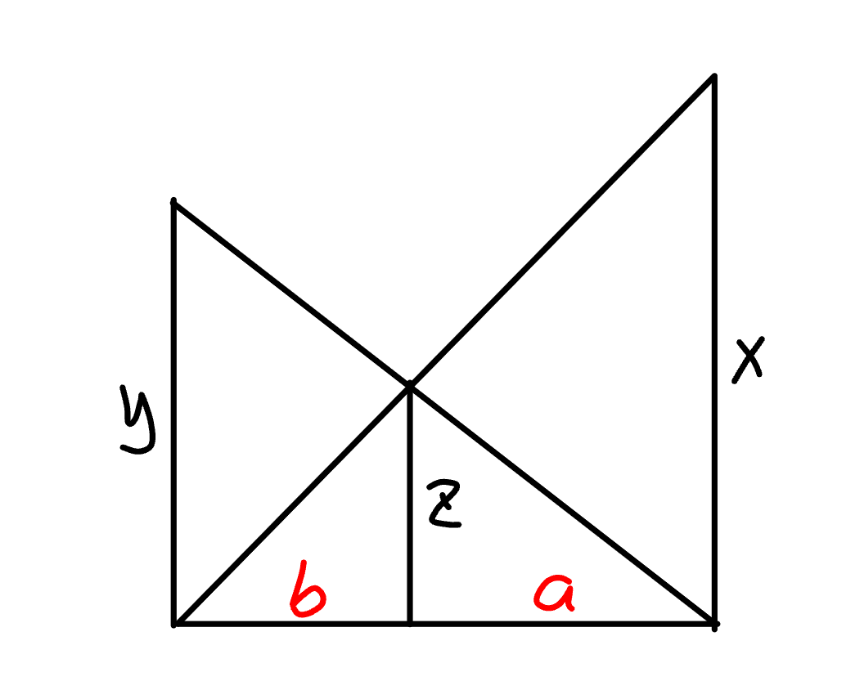
$$\frac{{x}}{{z}}=\frac{{a}+{b}}{{b}}=\mathrm{1}+\frac{{a}}{{b}}\:\Rightarrow\frac{{a}}{{b}}=\frac{{x}}{{z}}−\mathrm{1} \\ $$$$\frac{{y}}{{z}}=\frac{{a}+{b}}{{a}}=\mathrm{1}+\frac{{b}}{{a}}\:\Rightarrow\frac{{b}}{{a}}=\frac{{y}}{{z}}−\mathrm{1} \\ $$$$\Rightarrow\left(\frac{{x}}{{z}}−\mathrm{1}\right)\left(\frac{{y}}{{z}}−\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow{xy}=\left({x}+{y}\right){z} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:\checkmark \\ $$

Commented by peter frank last updated on 04/Aug/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by A5T last updated on 04/Aug/24

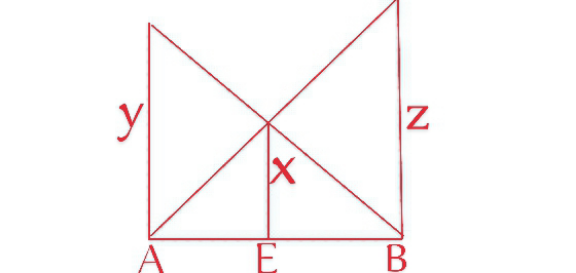
Commented by A5T last updated on 04/Aug/24

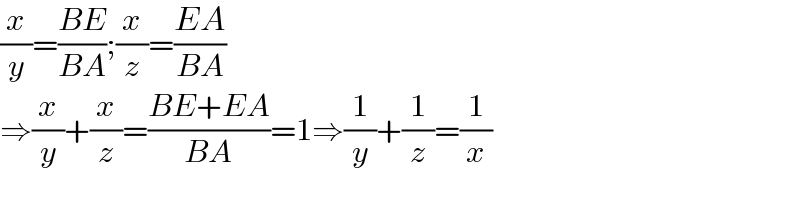
(x/y)=((BE)/(BA));(x/z)=((EA)/(BA)) ⇒(x/y)+(x/z)=((BE+EA)/(BA))=1⇒(1/y)+(1/z)=(1/x)

$$\frac{{x}}{{y}}=\frac{{BE}}{{BA}};\frac{{x}}{{z}}=\frac{{EA}}{{BA}} \\ $$$$\Rightarrow\frac{{x}}{{y}}+\frac{{x}}{{z}}=\frac{{BE}+{EA}}{{BA}}=\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{{x}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com