Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 210120 by emilagazade last updated on 31/Jul/24

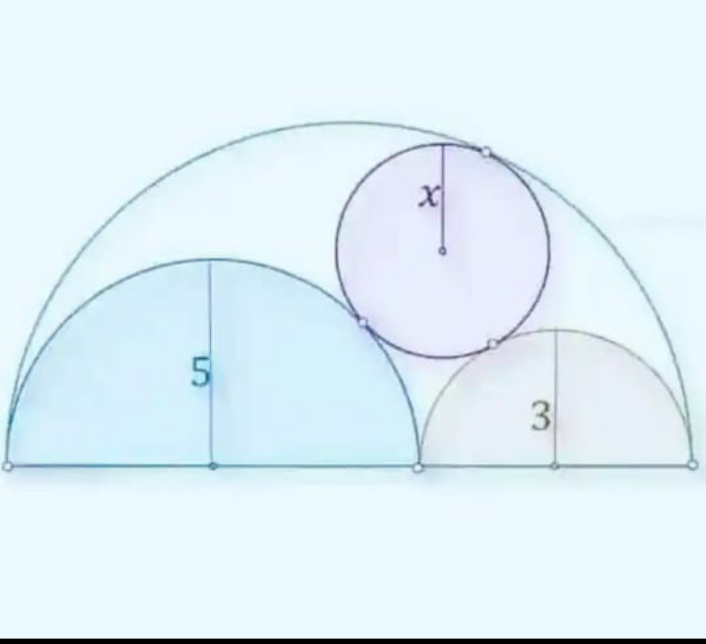
Answered by mr W last updated on 31/Jul/24

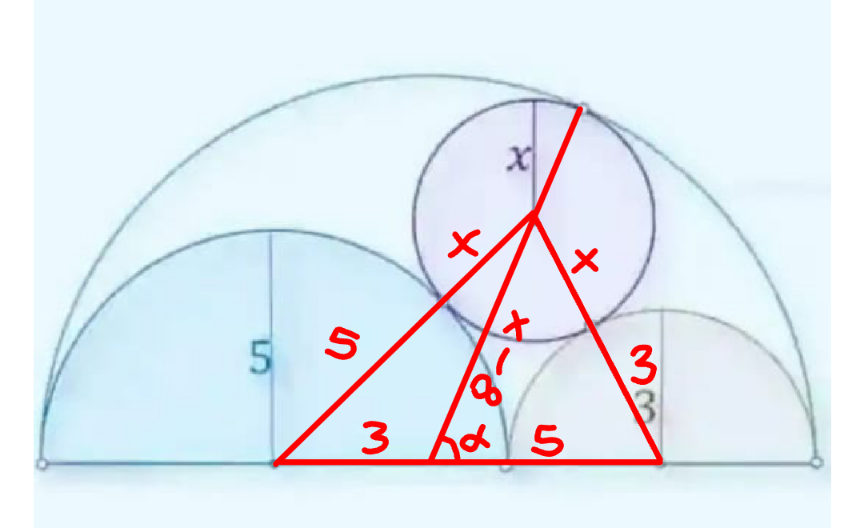
Commented by mr W last updated on 31/Jul/24

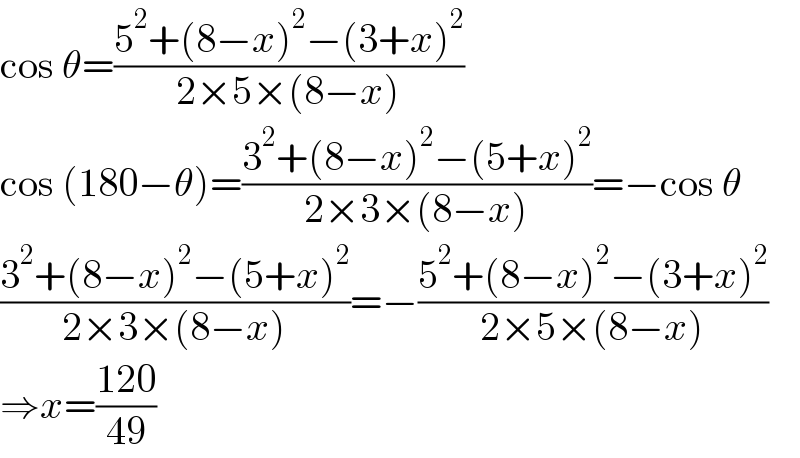
cos θ=((5^2 +(8−x)^2 −(3+x)^2 )/(2×5×(8−x))) cos (180−θ)=((3^2 +(8−x)^2 −(5+x)^2 )/(2×3×(8−x)))=−cos θ ((3^2 +(8−x)^2 −(5+x)^2 )/(2×3×(8−x)))=−((5^2 +(8−x)^2 −(3+x)^2 )/(2×5×(8−x))) ⇒x=((120)/(49))

$$\mathrm{cos}\:\theta=\frac{\mathrm{5}^{\mathrm{2}} +\left(\mathrm{8}−{x}\right)^{\mathrm{2}} −\left(\mathrm{3}+{x}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×\left(\mathrm{8}−{x}\right)} \\ $$$$\mathrm{cos}\:\left(\mathrm{180}−\theta\right)=\frac{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{8}−{x}\right)^{\mathrm{2}} −\left(\mathrm{5}+{x}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}×\left(\mathrm{8}−{x}\right)}=−\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{8}−{x}\right)^{\mathrm{2}} −\left(\mathrm{5}+{x}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}×\left(\mathrm{8}−{x}\right)}=−\frac{\mathrm{5}^{\mathrm{2}} +\left(\mathrm{8}−{x}\right)^{\mathrm{2}} −\left(\mathrm{3}+{x}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{5}×\left(\mathrm{8}−{x}\right)} \\ $$$$\Rightarrow{x}=\frac{\mathrm{120}}{\mathrm{49}} \\ $$

Answered by mr W last updated on 31/Jul/24

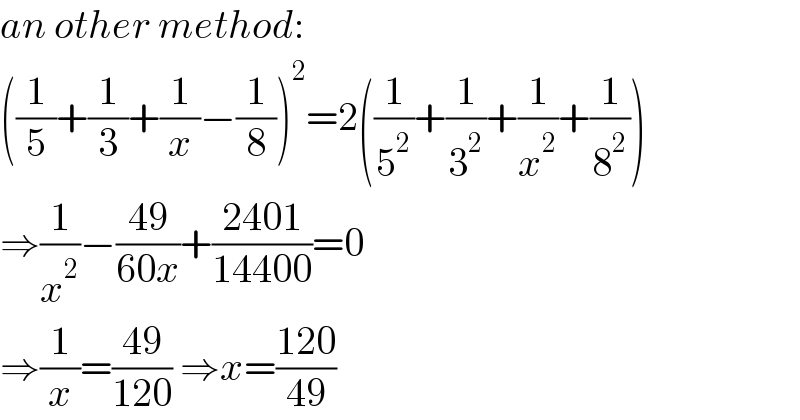
an other method: ((1/5)+(1/3)+(1/x)−(1/8))^2 =2((1/5^2 )+(1/3^2 )+(1/x^2 )+(1/8^2 )) ⇒(1/x^2 )−((49)/(60x))+((2401)/(14400))=0 ⇒(1/x)=((49)/(120)) ⇒x=((120)/(49))

$${an}\:{other}\:{method}: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{8}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{49}}{\mathrm{60}{x}}+\frac{\mathrm{2401}}{\mathrm{14400}}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{\mathrm{49}}{\mathrm{120}}\:\Rightarrow{x}=\frac{\mathrm{120}}{\mathrm{49}} \\ $$

Commented by emilagazade last updated on 31/Jul/24

thank you a lot Sir

$${thank}\:{you}\:{a}\:{lot}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com