Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

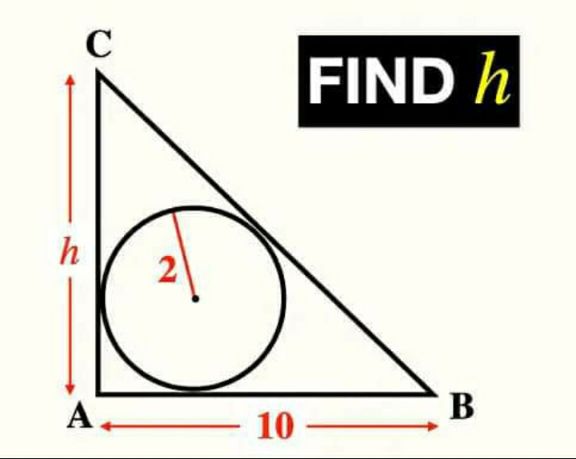
Question Number 210072 by peter frank last updated on 29/Jul/24

Answered by Frix last updated on 29/Jul/24

The incircle of a rectangular triangle with sides a, b, (√(a^2 +b^2 )) is ((a+b−(√(a^2 +b^2 )))/2) (∗) We have ((h+10−(√(h^2 +100)))/2)=2 ⇒ h+6=(√(h^2 +100)) ⇒ h=((16)/3) (∗) Incircle of a triangle =((2×area)/(circumference)) Area of a rectangular triangle =((ab)/2) ⇒ Incircle =((ab)/(2(a+b+(√(a^2 +b^2 )))))=the above

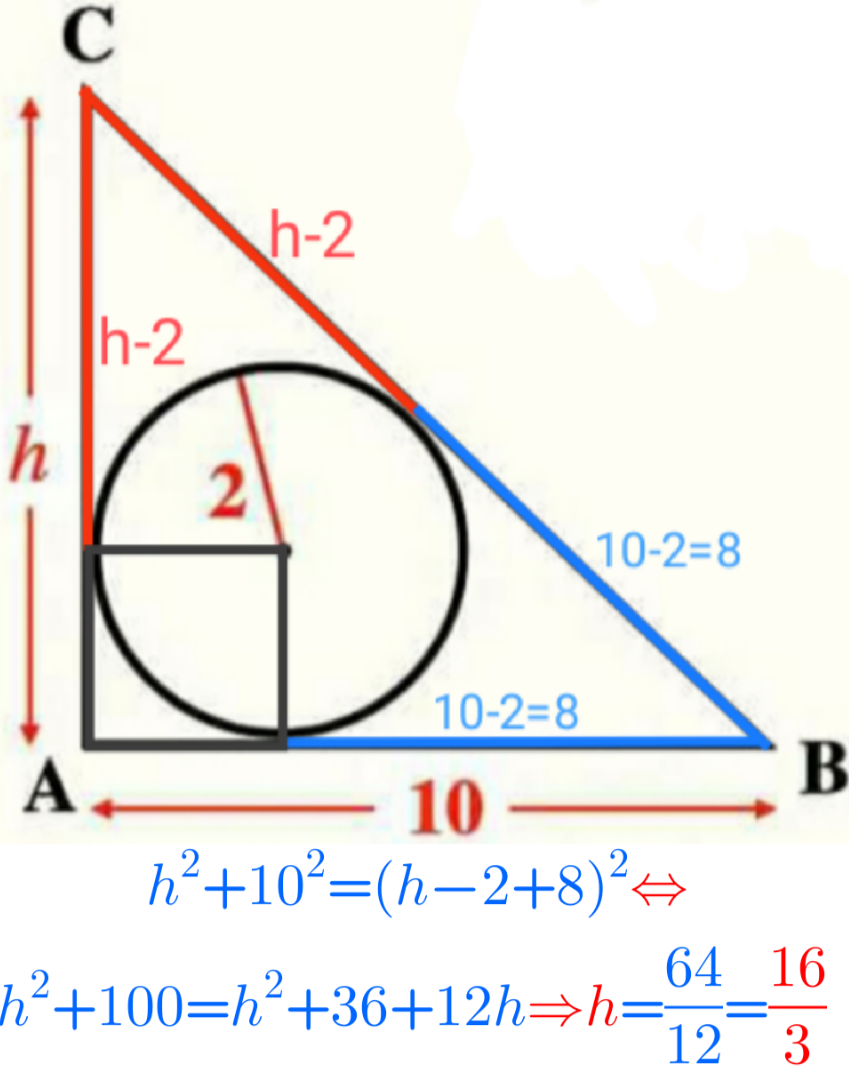
$$\mathrm{The}\:\mathrm{incircle}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rectangular}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\mathrm{sides}\:{a},\:{b},\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{is}\:\frac{{a}+{b}−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}}\:\:\:\:\:\left(\ast\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\frac{{h}+\mathrm{10}−\sqrt{{h}^{\mathrm{2}} +\mathrm{100}}}{\mathrm{2}}=\mathrm{2} \\ $$$$\Rightarrow\:{h}+\mathrm{6}=\sqrt{{h}^{\mathrm{2}} +\mathrm{100}}\:\Rightarrow\:{h}=\frac{\mathrm{16}}{\mathrm{3}} \\ $$$$ \\ $$$$\left(\ast\right)\:\mathrm{Incircle}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:=\frac{\mathrm{2}×\mathrm{area}}{\mathrm{circumference}} \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rectangular}\:\mathrm{triangle}\:=\frac{{ab}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{Incircle}\:=\frac{{ab}}{\mathrm{2}\left({a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)}=\mathrm{the}\:\mathrm{above} \\ $$

Answered by cherokeesay last updated on 29/Jul/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com