Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 210036 by peter frank last updated on 29/Jul/24

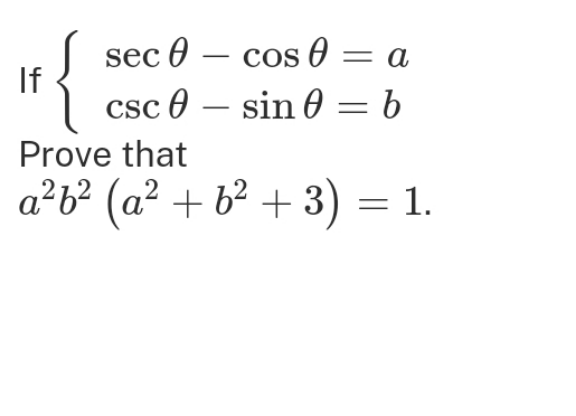
Answered by Prithwish last updated on 29/Jul/24

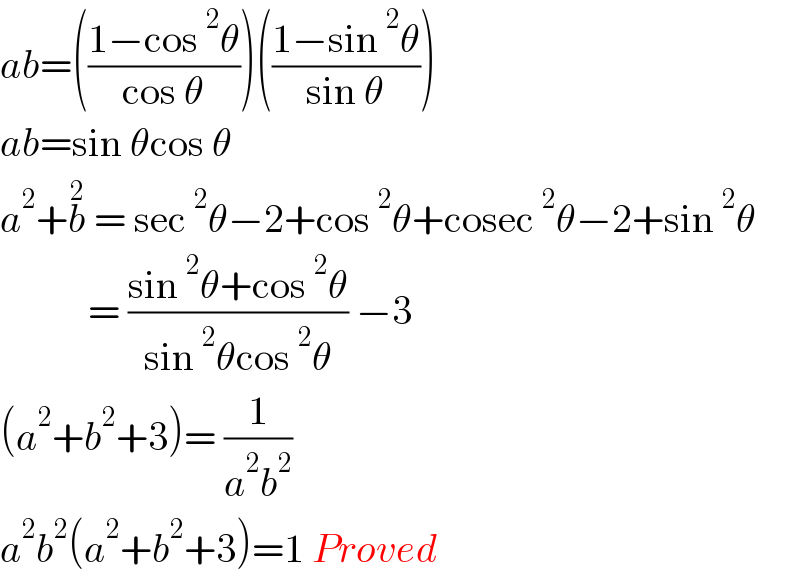
ab=(((1−cos^2 θ)/(cos θ)))(((1−sin^2 θ)/(sin θ))) ab=sin θcos θ a^2 +b^2 = sec^2 θ−2+cos^2 θ+cosec^2 θ−2+sin^2 θ = ((sin^2 θ+cos^2 θ)/(sin^2 θcos^2 θ)) −3 (a^2 +b^2 +3)= (1/(a^2 b^2 )) a^2 b^2 (a^2 +b^2 +3)=1 Proved

$${ab}=\left(\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:\theta}\right)\left(\frac{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:\theta}\right) \\ $$$${ab}=\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${a}^{\mathrm{2}} +\overset{\mathrm{2}} {{b}}\:=\:\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{2}+\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{cosec}\:^{\mathrm{2}} \theta−\mathrm{2}+\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta}\:−\mathrm{3} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}\right)=\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\: \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}\right)=\mathrm{1}\:{Proved} \\ $$

Commented by peter frank last updated on 29/Jul/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Frix last updated on 29/Jul/24

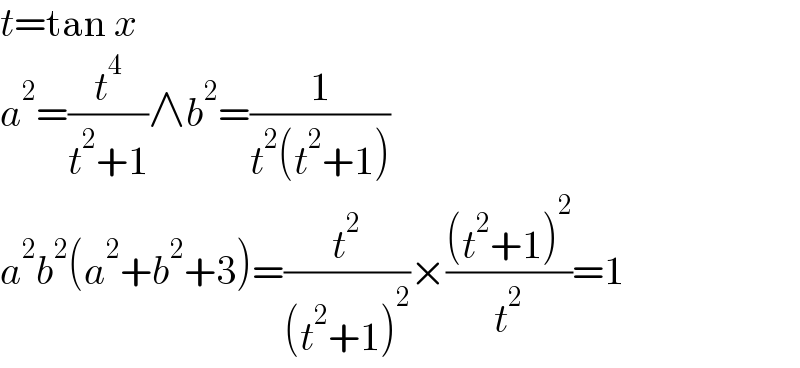
t=tan x a^2 =(t^4 /(t^2 +1))∧b^2 =(1/(t^2 (t^2 +1))) a^2 b^2 (a^2 +b^2 +3)=(t^2 /((t^2 +1)^2 ))×(((t^2 +1)^2 )/t^2 )=1

$${t}=\mathrm{tan}\:{x} \\ $$$${a}^{\mathrm{2}} =\frac{{t}^{\mathrm{4}} }{{t}^{\mathrm{2}} +\mathrm{1}}\wedge{b}^{\mathrm{2}} =\frac{\mathrm{1}}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}\right)=\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} }=\mathrm{1} \\ $$

Commented by peter frank last updated on 29/Jul/24

this very tough solution.can explain a little bit

$$\mathrm{this}\:\mathrm{very}\:\mathrm{tough}\:\mathrm{solution}.\mathrm{can}\:\mathrm{explain}\:\mathrm{a}\: \\ $$$$\mathrm{little}\:\mathrm{bit} \\ $$

Commented by Frix last updated on 29/Jul/24

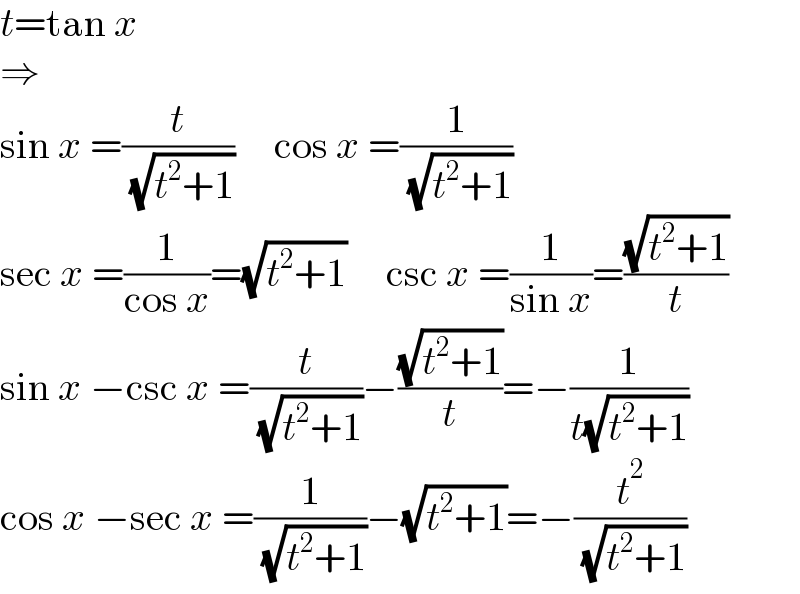
t=tan x ⇒ sin x =(t/( (√(t^2 +1)))) cos x =(1/( (√(t^2 +1)))) sec x =(1/(cos x))=(√(t^2 +1)) csc x =(1/(sin x))=((√(t^2 +1))/t) sin x −csc x =(t/( (√(t^2 +1))))−((√(t^2 +1))/t)=−(1/(t(√(t^2 +1)))) cos x −sec x =(1/( (√(t^2 +1))))−(√(t^2 +1))=−(t^2 /( (√(t^2 +1))))

$${t}=\mathrm{tan}\:{x} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}\:{x}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\:\:\:\:\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{sec}\:{x}\:=\frac{\mathrm{1}}{\mathrm{cos}\:{x}}=\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:\mathrm{csc}\:{x}\:=\frac{\mathrm{1}}{\mathrm{sin}\:{x}}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}} \\ $$$$\mathrm{sin}\:{x}\:−\mathrm{csc}\:{x}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}−\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{t}}=−\frac{\mathrm{1}}{{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{cos}\:{x}\:−\mathrm{sec}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}−\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}=−\frac{{t}^{\mathrm{2}} }{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$

Commented by peter frank last updated on 29/Jul/24

thank you for your clarification

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{your}\:\mathrm{clarification} \\ $$

Answered by Spillover last updated on 29/Jul/24

Commented by klipto last updated on 29/Jul/24

bro you niggerian?

$$\boldsymbol{\mathrm{bro}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{niggerian}}? \\ $$

Commented by peter frank last updated on 29/Jul/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Spillover last updated on 29/Jul/24

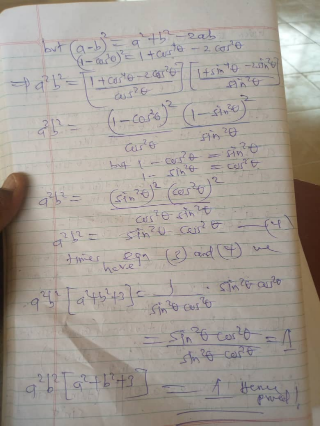
Commented by peter frank last updated on 29/Jul/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com