Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 209359 by peter frank last updated on 08/Jul/24

Commented by mr W last updated on 08/Jul/24

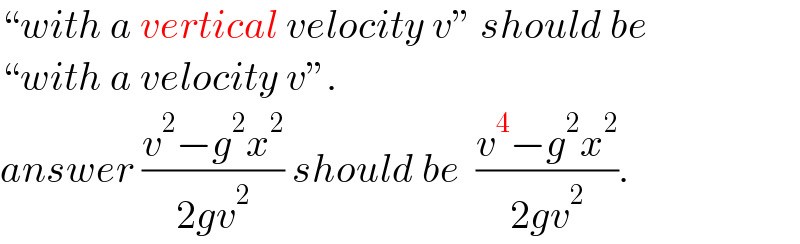
“with a vertical velocity v” should be “with a velocity v”. answer ((v^2 −g^2 x^2 )/(2gv^2 )) should be ((v^4 −g^2 x^2 )/(2gv^2 )).

$$``{with}\:{a}\:{vertical}\:{velocity}\:{v}''\:{should}\:{be} \\ $$$$``{with}\:{a}\:{velocity}\:{v}''. \\ $$$${answer}\:\frac{{v}^{\mathrm{2}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gv}^{\mathrm{2}} }\:{should}\:{be}\:\:\frac{{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gv}^{\mathrm{2}} }. \\ $$

Commented by peter frank last updated on 08/Jul/24

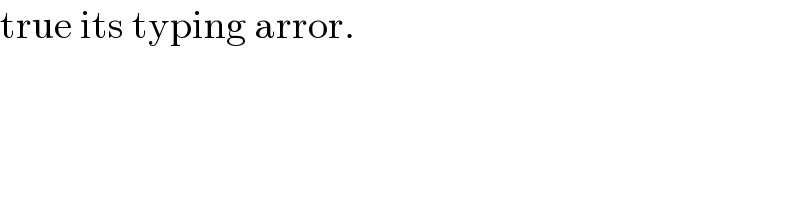
true its typing arror.

$$\mathrm{true}\:\mathrm{its}\:\mathrm{typing}\:\mathrm{arror}. \\ $$

Answered by Spillover last updated on 08/Jul/24

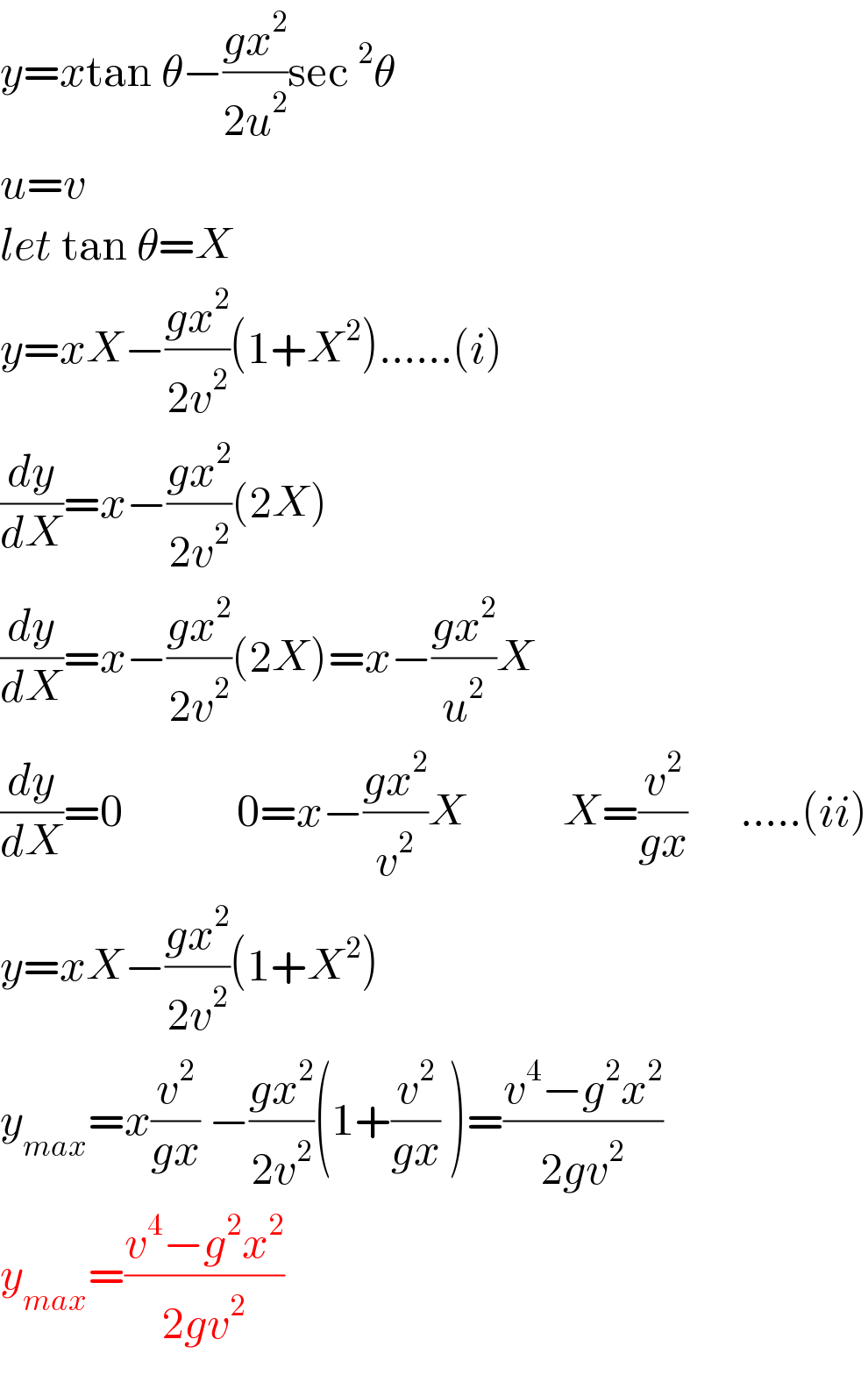
y=xtan θ−((gx^2 )/(2u^2 ))sec^2 θ u=v let tan θ=X y=xX−((gx^2 )/(2v^2 ))(1+X^2 )......(i) (dy/dX)=x−((gx^2 )/(2v^2 ))(2X) (dy/dX)=x−((gx^2 )/(2v^2 ))(2X)=x−((gx^2 )/u^2 )X (dy/dX)=0 0=x−((gx^2 )/v^2 )X X=(v^2 /(gx)) .....(ii) y=xX−((gx^2 )/(2v^2 ))(1+X^2 ) y_(max) =x(v^2 /(gx)) −((gx^2 )/(2v^2 ))(1+(v^2 /(gx)) )=((v^4 −g^2 x^2 )/(2gv^2 )) y_(max) =((v^4 −g^2 x^2 )/(2gv^2 ))

$${y}={x}\mathrm{tan}\:\theta−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }\mathrm{sec}\:^{\mathrm{2}} \theta \\ $$$${u}={v} \\ $$$${let}\:\mathrm{tan}\:\theta={X} \\ $$$${y}={xX}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+{X}^{\mathrm{2}} \right)......\left({i}\right) \\ $$$$\frac{{dy}}{{dX}}={x}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{2}{X}\right) \\ $$$$\frac{{dy}}{{dX}}={x}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{2}{X}\right)={x}−\frac{{gx}^{\mathrm{2}} }{{u}^{\mathrm{2}} }{X} \\ $$$$\frac{{dy}}{{dX}}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}={x}−\frac{{gx}^{\mathrm{2}} }{{v}^{\mathrm{2}} }{X}\:\:\:\:\:\:\:\:\:\:\:{X}=\frac{{v}^{\mathrm{2}} }{{gx}}\:\:\:\:\:\:.....\left({ii}\right) \\ $$$${y}={xX}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+{X}^{\mathrm{2}} \right) \\ $$$${y}_{{max}} ={x}\frac{{v}^{\mathrm{2}} }{{gx}}\:−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{v}^{\mathrm{2}} }{{gx}}\:\right)=\frac{{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gv}^{\mathrm{2}} } \\ $$$${y}_{{max}} =\frac{{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gv}^{\mathrm{2}} } \\ $$

Commented by Spillover last updated on 08/Jul/24

method 1

$${method}\:\mathrm{1} \\ $$

Commented by peter frank last updated on 08/Jul/24

thanks

$$\mathrm{thanks} \\ $$

Answered by Spillover last updated on 08/Jul/24

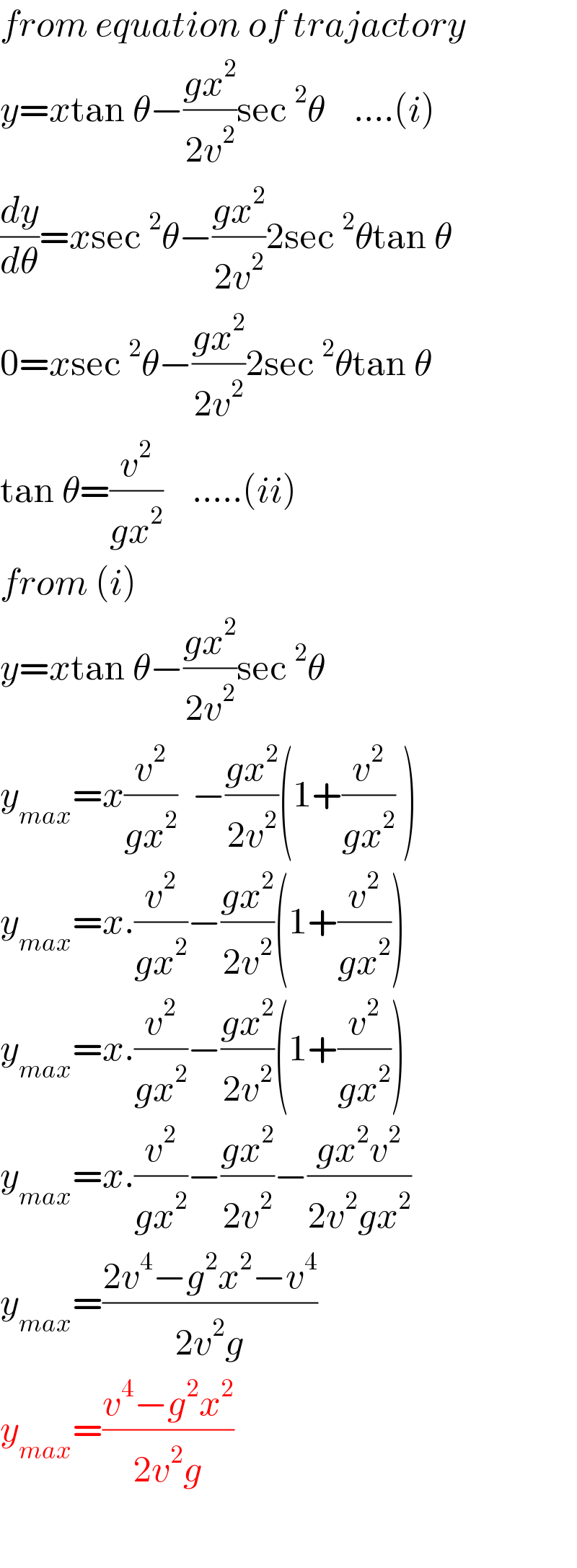
from equation of trajactory y=xtan θ−((gx^2 )/(2v^2 ))sec^2 θ ....(i) (dy/dθ)=xsec^2 θ−((gx^2 )/(2v^2 ))2sec^2 θtan θ 0=xsec^2 θ−((gx^2 )/(2v^2 ))2sec^2 θtan θ tan θ=(v^2 /(gx^2 )) .....(ii) from (i) y=xtan θ−((gx^2 )/(2v^2 ))sec^2 θ y_(max) =x(v^2 /(gx^2 )) −((gx^2 )/(2v^2 ))(1+(v^2 /(gx^2 )) ) y_(max) =x.(v^2 /(gx^2 ))−((gx^2 )/(2v^2 ))(1+(v^2 /(gx^2 ))) y_(max) =x.(v^2 /(gx^2 ))−((gx^2 )/(2v^2 ))(1+(v^2 /(gx^2 ))) y_(max) =x.(v^2 /(gx^2 ))−((gx^2 )/(2v^2 ))−((gx^2 v^2 )/(2v^2 gx^2 )) y_(max) =((2v^4 −g^2 x^2 −v^4 )/(2v^2 g)) y_(max) =((v^4 −g^2 x^2 )/(2v^2 g))

$${from}\:{equation}\:{of}\:{trajactory} \\ $$$${y}={x}\mathrm{tan}\:\theta−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\mathrm{sec}\:^{\mathrm{2}} \theta\:\:\:\:....\left({i}\right) \\ $$$$\frac{{dy}}{{d}\theta}={x}\mathrm{sec}\:^{\mathrm{2}} \theta−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\mathrm{2sec}\:^{\mathrm{2}} \theta\mathrm{tan}\:\theta \\ $$$$\mathrm{0}={x}\mathrm{sec}\:^{\mathrm{2}} \theta−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\mathrm{2sec}\:^{\mathrm{2}} \theta\mathrm{tan}\:\theta \\ $$$$\mathrm{tan}\:\theta=\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }\:\:\:\:.....\left({ii}\right) \\ $$$${from}\:\left({i}\right) \\ $$$${y}={x}\mathrm{tan}\:\theta−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\mathrm{sec}\:^{\mathrm{2}} \theta\:\:\:\: \\ $$$${y}_{{max}} ={x}\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }\:\:−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }\:\right) \\ $$$${y}_{{max}} ={x}.\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }\right) \\ $$$${y}_{{max}} ={x}.\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }\right) \\ $$$${y}_{{max}} ={x}.\frac{{v}^{\mathrm{2}} }{{gx}^{\mathrm{2}} }−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }−\frac{{gx}^{\mathrm{2}} {v}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} {gx}^{\mathrm{2}} } \\ $$$${y}_{{max}} =\frac{\mathrm{2}{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} −{v}^{\mathrm{4}} }{\mathrm{2}{v}^{\mathrm{2}} {g}} \\ $$$${y}_{{max}} =\frac{{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} {g}} \\ $$$$ \\ $$

Commented by Spillover last updated on 08/Jul/24

method 2

$${method}\:\mathrm{2} \\ $$

Answered by mr W last updated on 08/Jul/24

Commented by mr W last updated on 08/Jul/24

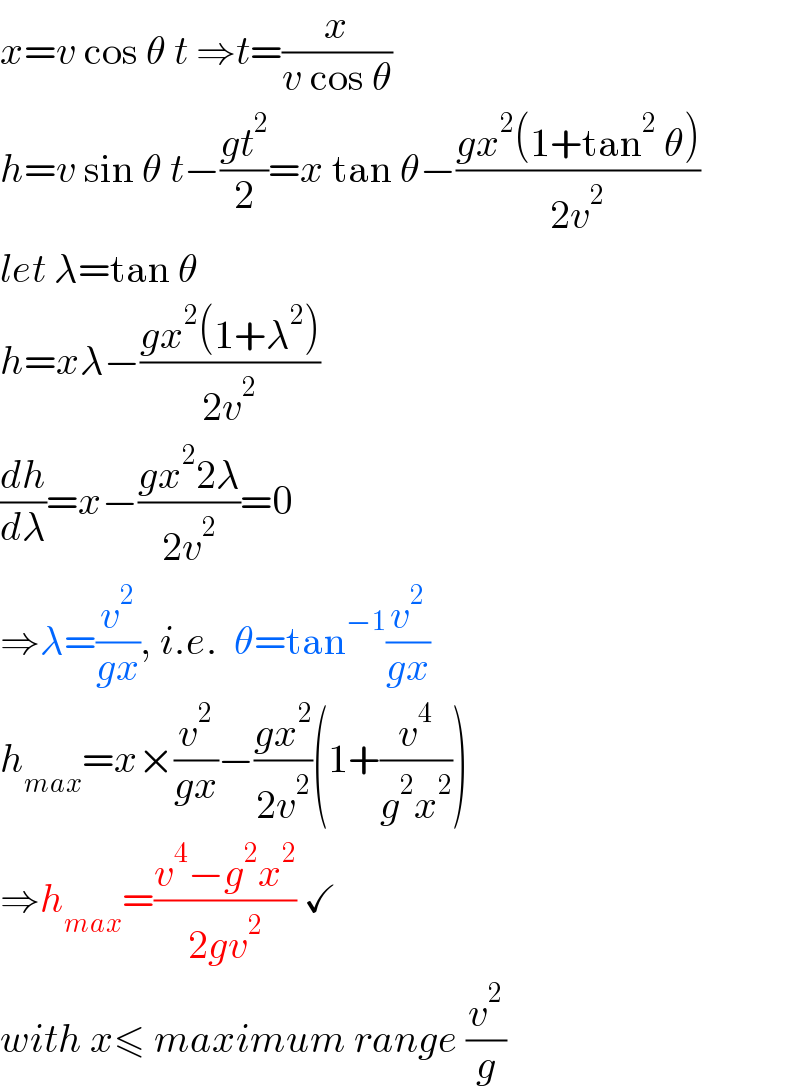
x=v cos θ t ⇒t=(x/(v cos θ)) h=v sin θ t−((gt^2 )/2)=x tan θ−((gx^2 (1+tan^2 θ))/(2v^2 )) let λ=tan θ h=xλ−((gx^2 (1+λ^2 ))/(2v^2 )) (dh/dλ)=x−((gx^2 2λ)/(2v^2 ))=0 ⇒λ=(v^2 /(gx)), i.e. θ=tan^(−1) (v^2 /(gx)) h_(max) =x×(v^2 /(gx))−((gx^2 )/(2v^2 ))(1+(v^4 /(g^2 x^2 ))) ⇒h_(max) =((v^4 −g^2 x^2 )/(2gv^2 )) ✓ with x≤ maximum range (v^2 /g)

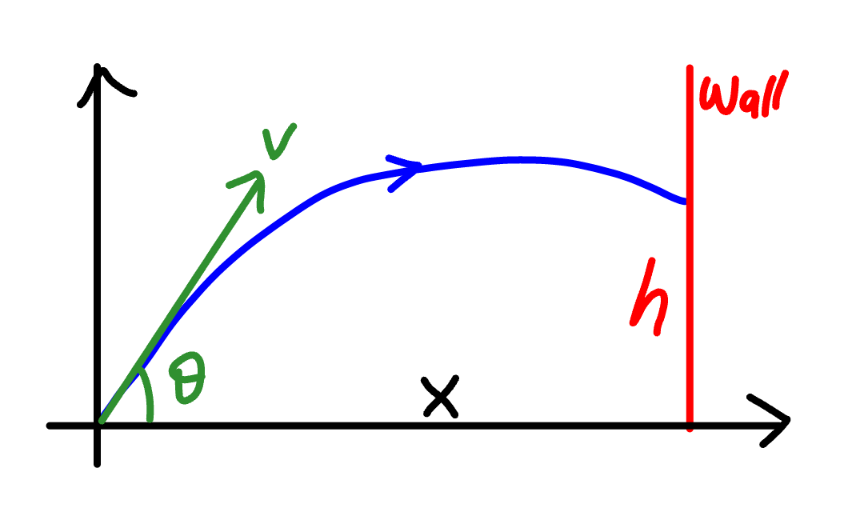
$${x}={v}\:\mathrm{cos}\:\theta\:{t}\:\Rightarrow{t}=\frac{{x}}{{v}\:\mathrm{cos}\:\theta} \\ $$$${h}={v}\:\mathrm{sin}\:\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}={x}\:\mathrm{tan}\:\theta−\frac{{gx}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{v}^{\mathrm{2}} } \\ $$$${let}\:\lambda=\mathrm{tan}\:\theta \\ $$$${h}={x}\lambda−\frac{{gx}^{\mathrm{2}} \left(\mathrm{1}+\lambda^{\mathrm{2}} \right)}{\mathrm{2}{v}^{\mathrm{2}} } \\ $$$$\frac{{dh}}{{d}\lambda}={x}−\frac{{gx}^{\mathrm{2}} \mathrm{2}\lambda}{\mathrm{2}{v}^{\mathrm{2}} }=\mathrm{0}\: \\ $$$$\Rightarrow\lambda=\frac{{v}^{\mathrm{2}} }{{gx}},\:{i}.{e}.\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{v}^{\mathrm{2}} }{{gx}} \\ $$$${h}_{{max}} ={x}×\frac{{v}^{\mathrm{2}} }{{gx}}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{v}^{\mathrm{4}} }{{g}^{\mathrm{2}} {x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{h}_{{max}} =\frac{{v}^{\mathrm{4}} −{g}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}{gv}^{\mathrm{2}} }\:\checkmark \\ $$$${with}\:{x}\leqslant\:{maximum}\:{range}\:\frac{{v}^{\mathrm{2}} }{{g}} \\ $$

Commented by peter frank last updated on 08/Jul/24

appriciate sir

$$\mathrm{appriciate}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com