
Question Number 209358 by peter frank last updated on 08/Jul/24

Commented by mr W last updated on 08/Jul/24

$${if}\:{the}\:{bowl}\:{is}\:{smooth},\:{why}\:{should}\:{the}\: \\ $$$${small}\:{block}\:{rotate}\:{with}\:{the}\:{bowl}\:{and} \\ $$$${not}\:{fall}\:{to}\:{the}\:{middle}\:{of}\:{the}\:{bowl}? \\ $$
Commented by mr W last updated on 08/Jul/24
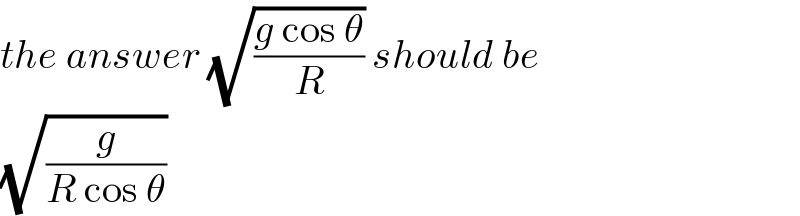
$${the}\:{answer}\:\sqrt{\frac{{g}\:\mathrm{cos}\:\theta}{{R}}}\:{should}\:{be} \\ $$$$\sqrt{\frac{{g}}{{R}\:\mathrm{cos}\:\theta}} \\ $$
Commented by mr W last updated on 08/Jul/24

$${what}\:{a}\:{book}\:{are}\:{you}\:{working}\:{with}? \\ $$$${it}\:{contains}\:{too}\:{many}\:{mistakes}! \\ $$
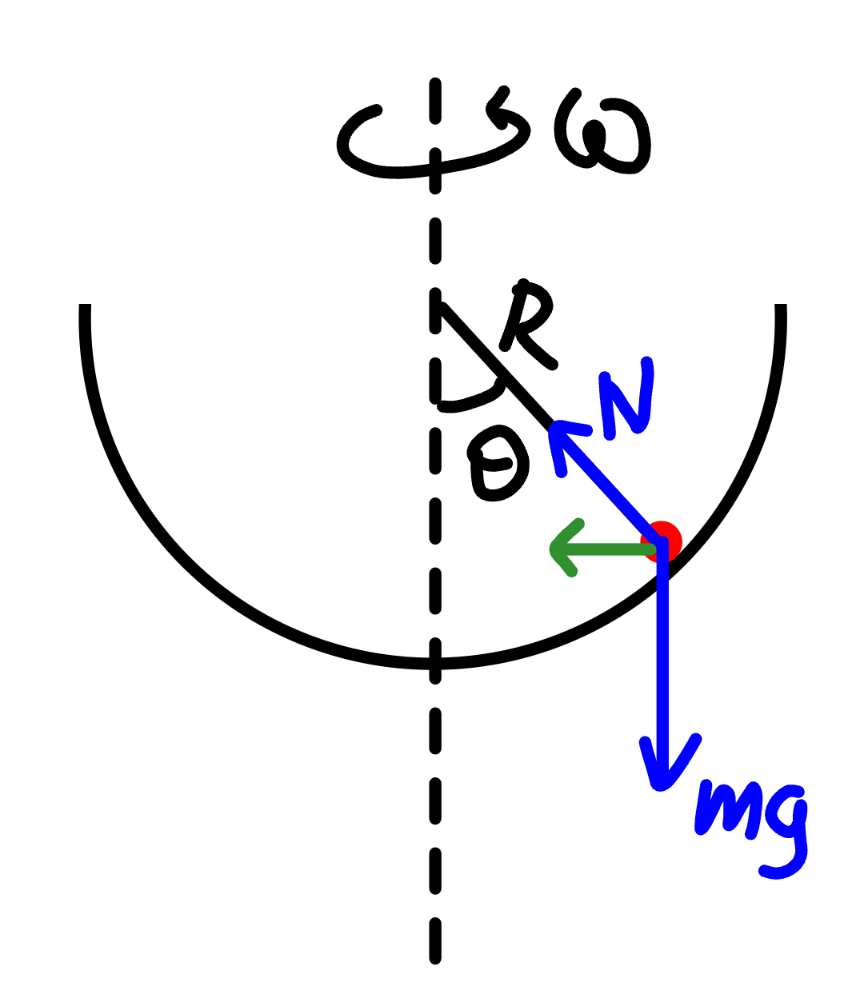
Answered by mr W last updated on 08/Jul/24
Commented by mr W last updated on 08/Jul/24
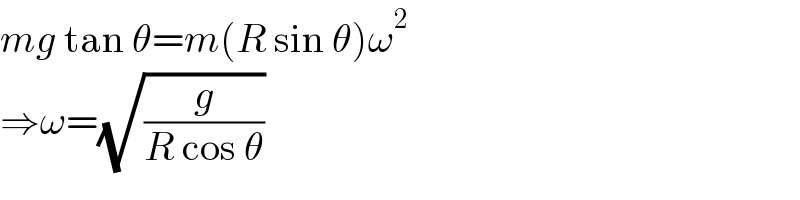
$${mg}\:\mathrm{tan}\:\theta={m}\left({R}\:\mathrm{sin}\:\theta\right)\omega^{\mathrm{2}} \\ $$$$\Rightarrow\omega=\sqrt{\frac{{g}}{{R}\:\mathrm{cos}\:\theta}} \\ $$
Commented by peter frank last updated on 08/Jul/24

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{the}\:\mathrm{solution}. \\ $$
