
Question Number 209352 by Spillover last updated on 07/Jul/24

Answered by mr W last updated on 08/Jul/24
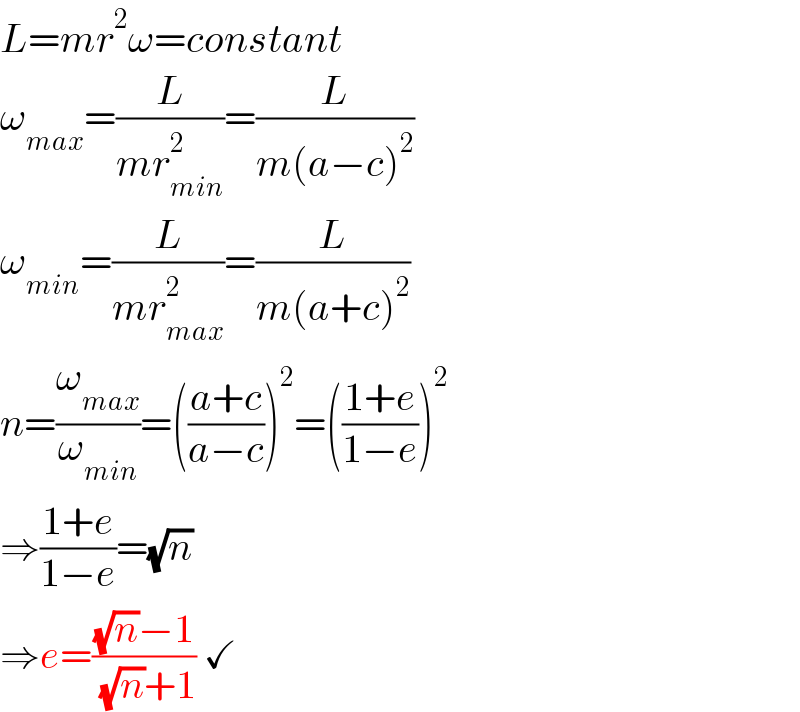
$${L}={mr}^{\mathrm{2}} \omega={constant} \\ $$$$\omega_{{max}} =\frac{{L}}{{mr}_{{min}} ^{\mathrm{2}} }=\frac{{L}}{{m}\left({a}−{c}\right)^{\mathrm{2}} } \\ $$$$\omega_{{min}} =\frac{{L}}{{mr}_{{max}} ^{\mathrm{2}} }=\frac{{L}}{{m}\left({a}+{c}\right)^{\mathrm{2}} } \\ $$$${n}=\frac{\omega_{{max}} }{\omega_{{min}} }=\left(\frac{{a}+{c}}{{a}−{c}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}+{e}}{\mathrm{1}−{e}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}+{e}}{\mathrm{1}−{e}}=\sqrt{{n}} \\ $$$$\Rightarrow{e}=\frac{\sqrt{{n}}−\mathrm{1}}{\:\sqrt{{n}}+\mathrm{1}}\:\checkmark \\ $$
Answered by Spillover last updated on 12/Jul/24

$${from}\:{conservation}\:{of}\:{angular}\:{momentum} \\ $$$${L}={mr}^{\mathrm{2}} \theta\:\:\:\:\:\: \\ $$$$\:\theta_{{max}} =\frac{{L}}{{mr}_{{max}} ^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta_{{min}} =\frac{{L}}{{mr}_{{min}} ^{\mathrm{2}} }\:\: \\ $$$${where}\:\:\:\:\:\:\:{r}_{{min}} ={a}\left(\mathrm{1}−{e}\right)\:\:\:\:\:\:\:\:\:\:{r}_{{max}} ={a}\left(\mathrm{1}+{e}\right) \\ $$$${ratio}\:{of}\:{angular}\:{velocity}\:\left({n}\right) \\ $$$${n}=\frac{\:\theta_{{max}} =\frac{{L}}{{mr}_{{max}} ^{\mathrm{2}} }\:\:\:}{\:\theta_{{min}} =\frac{{L}}{{mr}_{{min}} ^{\mathrm{2}} }\:\:}=\frac{\theta_{{max}} }{\theta_{{min}} }=\frac{{r}_{{max}} ^{\mathrm{2}} }{{r}_{{min}} ^{\mathrm{2}} } \\ $$$${n}=\left(\frac{\mathrm{1}+{e}}{\mathrm{1}−{e}}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\sqrt{{n}}=\:\:\:\:\frac{\mathrm{1}+{e}}{\mathrm{1}−{e}}\:\:\:\:\:\:\:\: \\ $$$$\sqrt{{n}}\:\left(\mathrm{1}−{e}\right)=\mathrm{1}+{e} \\ $$$${e}=\frac{\sqrt{{n}}−\mathrm{1}}{\:\sqrt{{n}}+\mathrm{1}} \\ $$
