
Question Number 209347 by RoseAli last updated on 07/Jul/24
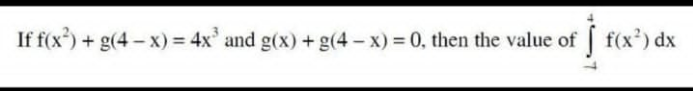
Answered by Berbere last updated on 07/Jul/24
![∫_(−4) ^4 f(x)dx=2∫^4 _0 f(x^2 )dx ∫_0 ^4 g(x)dx=∫_0 ^4 g(4−x)⇒2∫_0 ^4 g(x)=∫_0 ^4 g(x)+g(4−x)dx=0 ⇒2∫_0 ^4 f(x^2 )+g(x)dx=2∫_0 ^4 f(x^2 )dx=∫_0 ^4 8x^3 =2[x^4 ]_0 ^4 =512](Q209348.png)
$$\int_{−\mathrm{4}} ^{\mathrm{4}} {f}\left({x}\right){dx}=\mathrm{2}\underset{\mathrm{0}} {\int}^{\mathrm{4}} {f}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} {g}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{4}} {g}\left(\mathrm{4}−{x}\right)\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{4}} {g}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{4}} {g}\left({x}\right)+{g}\left(\mathrm{4}−{x}\right){dx}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}^{\mathrm{2}} \right)+{g}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}^{\mathrm{2}} \right){dx}=\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{8}{x}^{\mathrm{3}} =\mathrm{2}\left[{x}^{\mathrm{4}} \right]_{\mathrm{0}} ^{\mathrm{4}} =\mathrm{512} \\ $$$$ \\ $$
