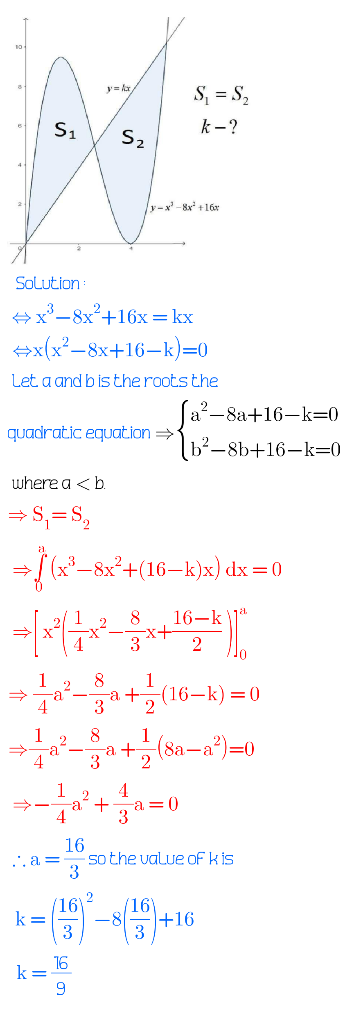Question Number 209332 by efronzo1 last updated on 07/Jul/24
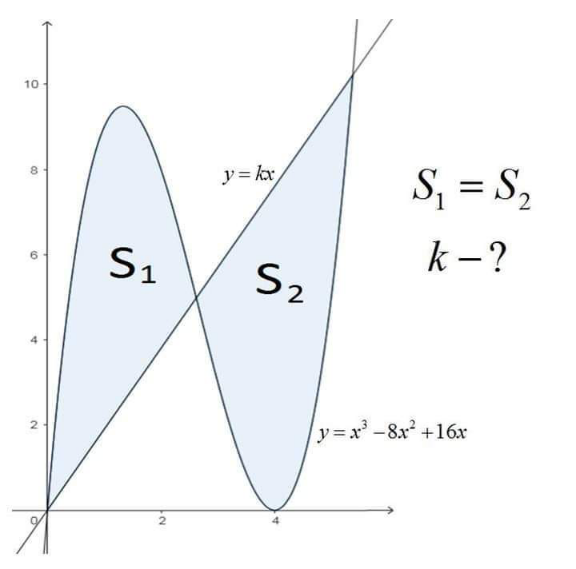
Answered by Frix last updated on 07/Jul/24
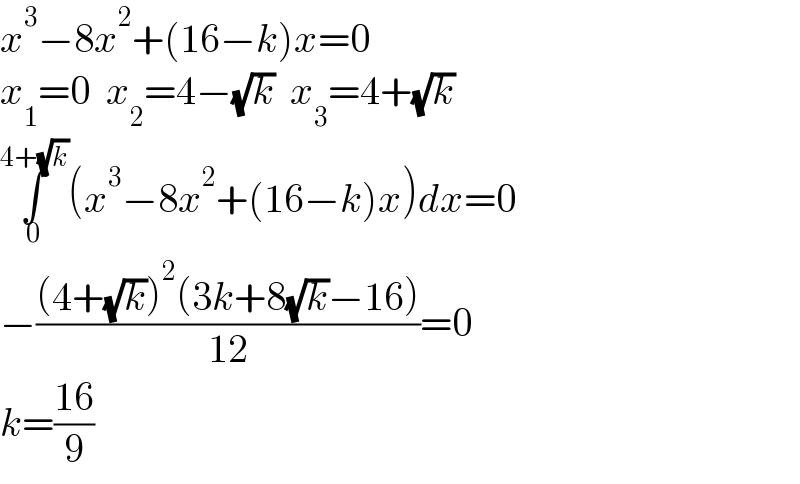
$${x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\left(\mathrm{16}−{k}\right){x}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}\:\:{x}_{\mathrm{2}} =\mathrm{4}−\sqrt{{k}}\:\:{x}_{\mathrm{3}} =\mathrm{4}+\sqrt{{k}} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{4}+\sqrt{{k}}} {\int}}\left({x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\left(\mathrm{16}−{k}\right){x}\right){dx}=\mathrm{0} \\ $$$$−\frac{\left(\mathrm{4}+\sqrt{{k}}\right)^{\mathrm{2}} \left(\mathrm{3}{k}+\mathrm{8}\sqrt{{k}}−\mathrm{16}\right)}{\mathrm{12}}=\mathrm{0} \\ $$$${k}=\frac{\mathrm{16}}{\mathrm{9}} \\ $$
Answered by MM42 last updated on 07/Jul/24
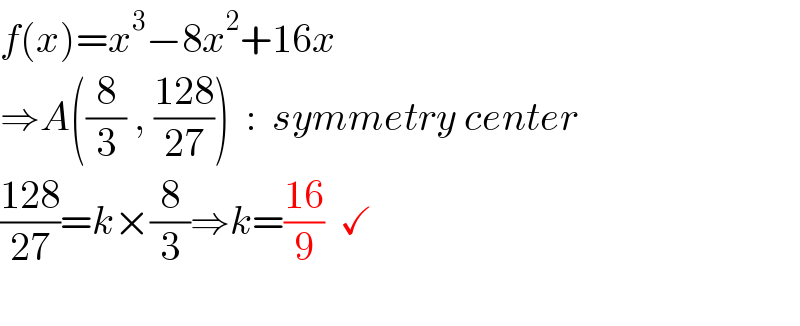
$${f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16}{x} \\ $$$$\Rightarrow{A}\left(\frac{\mathrm{8}}{\mathrm{3}}\:,\:\frac{\mathrm{128}}{\mathrm{27}}\right)\:\::\:\:{symmetry}\:{center} \\ $$$$\frac{\mathrm{128}}{\mathrm{27}}={k}×\frac{\mathrm{8}}{\mathrm{3}}\Rightarrow{k}=\frac{\mathrm{16}}{\mathrm{9}}\:\:\checkmark \\ $$$$ \\ $$
Answered by efronzo1 last updated on 08/Jul/24