Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 209314 by SonGoku last updated on 06/Jul/24

Commented by SonGoku last updated on 06/Jul/24

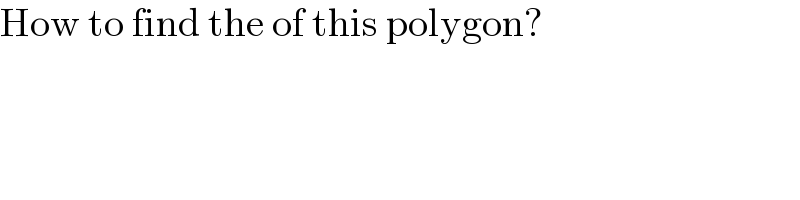
How to find the of this polygon?

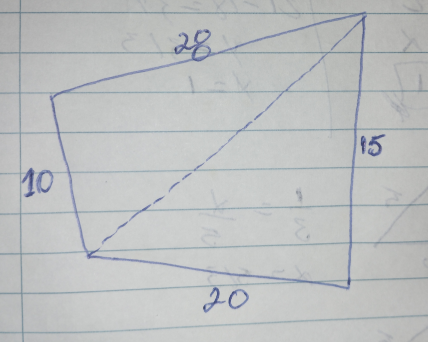
$$\mathrm{How}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{of}\:\mathrm{this}\:\mathrm{polygon}? \\ $$

Commented by mr W last updated on 07/Jul/24

you can only find the perimeter of the polygon, nothing else of it.

$${you}\:{can}\:{only}\:{find}\:{the}\:{perimeter}\:{of} \\ $$$${the}\:{polygon},\:{nothing}\:{else}\:{of}\:{it}. \\ $$

Commented by SonGoku last updated on 07/Jul/24

So the only way to determine the diagonal of ang irreular polygon, like the one in the image, is onlyo thrugh practice? In other words, in the field?

$$\mathrm{So}\:\mathrm{the}\:\mathrm{only}\:\mathrm{way}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{diagonal}\:\mathrm{of}\:\mathrm{ang} \\ $$$$\mathrm{irreular}\:\mathrm{polygon},\:\mathrm{like}\:\mathrm{the}\:\mathrm{one}\:\mathrm{in}\:\mathrm{the}\:\mathrm{image},\:\mathrm{is}\:\mathrm{onlyo} \\ $$$$\mathrm{thrugh}\:\mathrm{practice}?\:\mathrm{In}\:\mathrm{other}\:\mathrm{words},\:\mathrm{in}\:\mathrm{the}\:\mathrm{field}? \\ $$

Commented by Frix last updated on 07/Jul/24

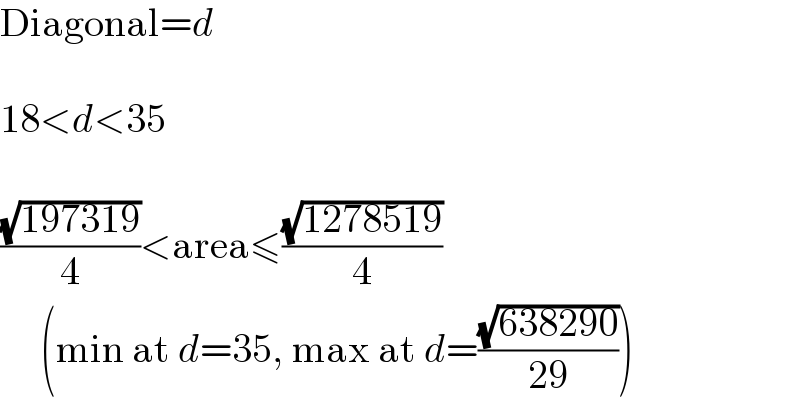
Diagonal=d 18<d<35 ((√(197319))/4)<area≤((√(1278519))/4) (min at d=35, max at d=((√(638290))/(29)))

$$\mathrm{Diagonal}={d} \\ $$$$ \\ $$$$\mathrm{18}<{d}<\mathrm{35} \\ $$$$ \\ $$$$\frac{\sqrt{\mathrm{197319}}}{\mathrm{4}}<\mathrm{area}\leqslant\frac{\sqrt{\mathrm{1278519}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\left(\mathrm{min}\:\mathrm{at}\:{d}=\mathrm{35},\:\mathrm{max}\:\mathrm{at}\:{d}=\frac{\sqrt{\mathrm{638290}}}{\mathrm{29}}\right) \\ $$

Commented by Frix last updated on 07/Jul/24

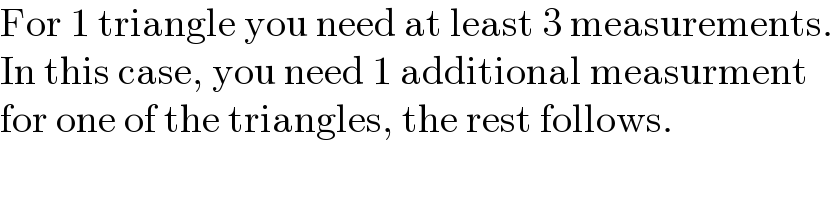
For 1 triangle you need at least 3 measurements. In this case, you need 1 additional measurment for one of the triangles, the rest follows.

$$\mathrm{For}\:\mathrm{1}\:\mathrm{triangle}\:\mathrm{you}\:\mathrm{need}\:\mathrm{at}\:\mathrm{least}\:\mathrm{3}\:\mathrm{measurements}. \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case},\:\mathrm{you}\:\mathrm{need}\:\mathrm{1}\:\mathrm{additional}\:\mathrm{measurment} \\ $$$$\mathrm{for}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangles},\:\mathrm{the}\:\mathrm{rest}\:\mathrm{follows}. \\ $$

Commented by SonGoku last updated on 08/Jul/24

But, how did you at these calculations?

$$\mathrm{But},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{at}\:\mathrm{these}\:\mathrm{calculations}? \\ $$

Commented by Frix last updated on 08/Jul/24

1^(st) triangle 10, 28, d ⇒ 18<d<38 2^(nd) triangle 15, 20, d ⇒ 5<d<35 ⇒ 18<d<35 Area of triangle a, b, c =((√((a+b+c)(b+c−a)(a+c−b)(a+b−c)))/4) Area of 1^(st) triangle A_1 =((√(−d^4 +1768d^2 −467856))/4) Area of 2^(nd) triangle A_2 =((√(−d^4 +1250d^2 −30625))/4) For the minimum obviously d=18 ⇒ A_1 =0 For the maximum I used differentiation

$$\mathrm{1}^{\mathrm{st}} \:\mathrm{triangle}\:\mathrm{10},\:\mathrm{28},\:{d}\:\Rightarrow\:\mathrm{18}<{d}<\mathrm{38} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{triangle}\:\mathrm{15},\:\mathrm{20},\:{d}\:\Rightarrow\:\mathrm{5}<{d}<\mathrm{35} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{18}<{d}<\mathrm{35} \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{triangle}\:{a},\:{b},\:{c} \\ $$$$\:\:\:\:\:=\frac{\sqrt{\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right)\left({a}+{c}−{b}\right)\left({a}+{b}−{c}\right)}}{\mathrm{4}} \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{triangle} \\ $$$$\:\:\:\:\:{A}_{\mathrm{1}} =\frac{\sqrt{−{d}^{\mathrm{4}} +\mathrm{1768}{d}^{\mathrm{2}} −\mathrm{467856}}}{\mathrm{4}} \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{triangle} \\ $$$$\:\:\:\:\:{A}_{\mathrm{2}} =\frac{\sqrt{−{d}^{\mathrm{4}} +\mathrm{1250}{d}^{\mathrm{2}} −\mathrm{30625}}}{\mathrm{4}} \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{obviously}\:{d}=\mathrm{18}\:\Rightarrow\:{A}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{I}\:\mathrm{used}\:\mathrm{differentiation} \\ $$

Commented by mr W last updated on 08/Jul/24

maximum area is when the quadilateral is cyclic. s=((a+b+c+d)/2)=((10+28+15+20)/2)=36.5 A_(max) =(√((s−a)(s−b)(s−c)(s−d))) =(√((36.5−10)(36.5−28)(36.5−15)(36.5−20))) =((√(1278519))/4) see also Q30233

$${maximum}\:{area}\:{is}\:{when}\:{the} \\ $$$${quadilateral}\:{is}\:{cyclic}. \\ $$$${s}=\frac{{a}+{b}+{c}+{d}}{\mathrm{2}}=\frac{\mathrm{10}+\mathrm{28}+\mathrm{15}+\mathrm{20}}{\mathrm{2}}=\mathrm{36}.\mathrm{5} \\ $$$${A}_{{max}} =\sqrt{\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)\left({s}−{d}\right)} \\ $$$$\:\:\:=\sqrt{\left(\mathrm{36}.\mathrm{5}−\mathrm{10}\right)\left(\mathrm{36}.\mathrm{5}−\mathrm{28}\right)\left(\mathrm{36}.\mathrm{5}−\mathrm{15}\right)\left(\mathrm{36}.\mathrm{5}−\mathrm{20}\right)} \\ $$$$\:\:\:=\frac{\sqrt{\mathrm{1278519}}}{\mathrm{4}} \\ $$$${see}\:{also}\:{Q}\mathrm{30233} \\ $$

Commented by SonGoku last updated on 09/Jul/24

Very sophisticated. Congratulations I willa study. Thank you.

$$\mathrm{Very}\:\mathrm{sophisticated}.\: \\ $$$$\mathrm{Congratulations} \\ $$$$\mathrm{I}\:\mathrm{willa}\:\mathrm{study}. \\ $$$$\mathrm{Thank}\:\mathrm{you}. \\ $$

Commented by SonGoku last updated on 09/Jul/24

So, can I use this formula to determine the area of any quadrilateral?

$$\mathrm{So},\:\mathrm{can}\:\mathrm{I}\:\mathrm{use}\:\mathrm{this}\:\mathrm{formula}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of} \\ $$$$\mathrm{any}\:\mathrm{quadrilateral}? \\ $$

Commented by mr W last updated on 09/Jul/24

no! it′s only for so−called cyclic quadrilaterals. generally a quadrilateral is not uniquely defined when only its four sides are given. you need an additional condition.

$${no}!\:{it}'{s}\:{only}\:{for}\:{so}−{called}\:{cyclic} \\ $$$${quadrilaterals}. \\ $$$${generally}\:{a}\:{quadrilateral}\:{is}\:{not} \\ $$$${uniquely}\:{defined}\:{when}\:{only}\:{its}\:{four} \\ $$$${sides}\:{are}\:{given}.\:{you}\:{need}\:{an} \\ $$$${additional}\:{condition}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com