
Question Number 209272 by Tawa11 last updated on 05/Jul/24
Commented by Tawa11 last updated on 05/Jul/24
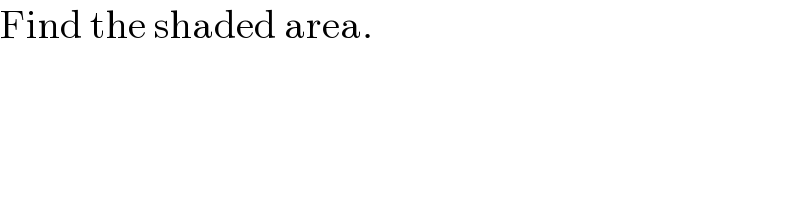
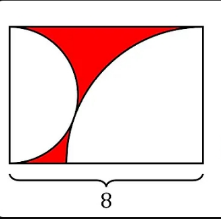
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{shaded}\:\mathrm{area}. \\ $$
Answered by A5T last updated on 05/Jul/24
![(r+R)^2 =r^2 +8^2 ⇒2rR+R^2 =64 2r=R⇒2R^2 =64⇒R=4(√2)⇒r=2(√2) ⇒[Red]=8×2r−((πr^2 )/2)−((πR^2 )/4)=32(√2)−12π](Q209274.png)
$$\left({r}+{R}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{rR}+{R}^{\mathrm{2}} =\mathrm{64} \\ $$$$\mathrm{2}{r}={R}\Rightarrow\mathrm{2}{R}^{\mathrm{2}} =\mathrm{64}\Rightarrow{R}=\mathrm{4}\sqrt{\mathrm{2}}\Rightarrow{r}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\left[{Red}\right]=\mathrm{8}×\mathrm{2}{r}−\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi{R}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{32}\sqrt{\mathrm{2}}−\mathrm{12}\pi \\ $$
Commented by Tawa11 last updated on 05/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
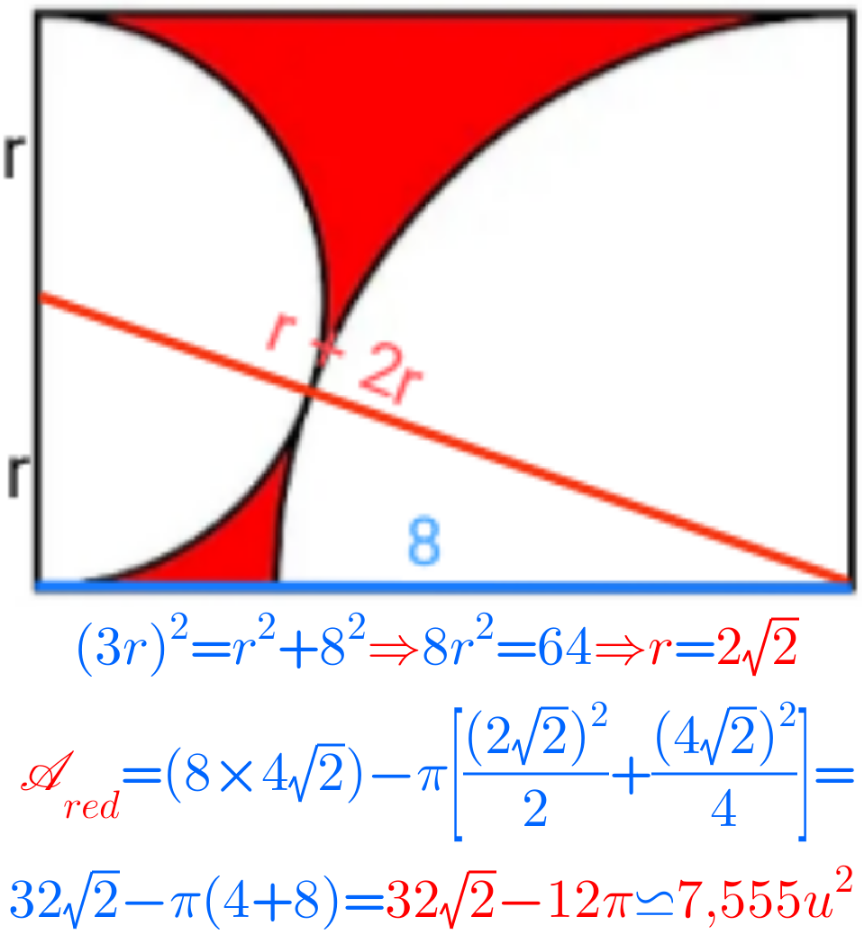
Answered by cherokeesay last updated on 06/Jul/24
Commented by Tawa11 last updated on 06/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
