
Question Number 209229 by Tawa11 last updated on 04/Jul/24
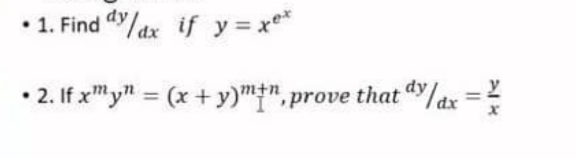
Commented by klipto last updated on 06/Jul/24
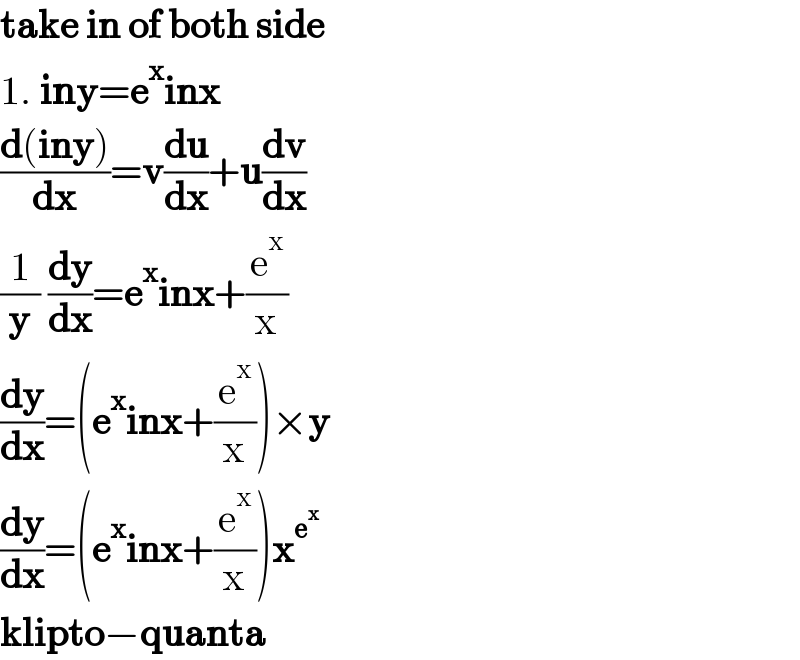
$$\boldsymbol{\mathrm{take}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{both}}\:\boldsymbol{\mathrm{side}} \\ $$$$\mathrm{1}.\:\boldsymbol{\mathrm{iny}}=\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{inx}} \\ $$$$\frac{\boldsymbol{\mathrm{d}}\left(\boldsymbol{\mathrm{iny}}\right)}{\boldsymbol{\mathrm{dx}}}=\boldsymbol{\mathrm{v}}\frac{\boldsymbol{\mathrm{du}}}{\boldsymbol{\mathrm{dx}}}+\boldsymbol{\mathrm{u}}\frac{\boldsymbol{\mathrm{dv}}}{\boldsymbol{\mathrm{dx}}} \\ $$$$\frac{\mathrm{1}}{\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{inx}}+\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{inx}}+\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}}\right)×\boldsymbol{\mathrm{y}} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{inx}}+\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}}\right)\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} } \\ $$$$\boldsymbol{\mathrm{klipto}}−\boldsymbol{\mathrm{quanta}} \\ $$
Commented by klipto last updated on 06/Jul/24
=[1+(dy/dx)](1/(x+y)) (m/x)+(n/y) (dy/dx)=(m+n)[1+(dy/dx)](1/(x+y)) (m/x)+(n/y) (dy/dx)=(m+n)[(1/(x+y))+(1/(x+y)) (dy/dx)] (n/y) (dy/dx)−((m+n)/(x+y)) (dy/dx)=((m+n)/(x+y))−(m/x) [(n/y)−((m+n)/(x+y))](dy/dx)=((m+n)/(x+y))−(m/x) ((n(x+y)−y(m+n))/(y(x+y))) (dy/dx)=((x(m+n)−m(x+y))/(x(x+y))) (dy/dx)=((x(m+n)−m(x+y))/(x(x+y)))÷((n(x+y)−y(m+n))/(y(x+y))) (dy/dx)=((mx+nx−mx−my)/(x^2 +xy))×((xy+y^2 )/(nx+ny−my−ny)) (dy/dx)=((nx−my)/(x^2 +xy))×((xy+y^2 )/(nx−my)) (dy/dx)=((xy+y^2 )/(x^2 +xy))=((y(x+y))/(x(x+y)))=(y/x) klipto−quanta](Q209287.png)
$$\mathrm{2}.\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{m}}} \boldsymbol{\mathrm{y}}^{\boldsymbol{\mathrm{n}}} =\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)^{\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}} \\ $$$$\boldsymbol{\mathrm{take}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{B}}.\boldsymbol{\mathrm{S}} \\ $$$$\boldsymbol{\mathrm{in}}\left(\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{m}}} \boldsymbol{\mathrm{y}}^{\boldsymbol{\mathrm{n}}} \right)=\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)\boldsymbol{\mathrm{in}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right) \\ $$$$\left(\boldsymbol{\mathrm{quick}}\:\boldsymbol{\mathrm{one}}:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{in}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right),?\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{u}}=\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}},\frac{\boldsymbol{\mathrm{du}}}{\boldsymbol{\mathrm{dx}}\:}=\mathrm{1}+\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right. \\ $$$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{inu}},\frac{\mathrm{dy}}{\mathrm{du}}=\frac{\mathrm{1}}{\boldsymbol{\mathrm{u}}},\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{du}}}{\boldsymbol{\mathrm{dx}}}×\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{du}}}=\left[\mathrm{1}+\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right]\frac{\mathrm{1}}{\boldsymbol{\mathrm{u}}}=\left[\mathrm{1}+\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right]\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}} \\ $$$$ \\ $$$$\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{x}}}+\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)\left[\mathrm{1}+\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right]\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}} \\ $$$$\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{x}}}+\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)\left[\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right] \\ $$$$\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}−\frac{\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}−\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{x}}} \\ $$$$\left[\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{y}}}−\frac{\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}\right]\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}−\frac{\boldsymbol{\mathrm{m}}}{\boldsymbol{\mathrm{x}}} \\ $$$$\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)−\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)}{\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)−\boldsymbol{\mathrm{m}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)−\boldsymbol{\mathrm{m}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}\boldsymbol{\div}\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)−\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{m}}+\boldsymbol{\mathrm{n}}\right)}{\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{mx}}+\boldsymbol{\mathrm{nx}}−\boldsymbol{\mathrm{mx}}−\boldsymbol{\mathrm{my}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}}×\frac{\boldsymbol{\mathrm{xy}}+\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\boldsymbol{\mathrm{nx}}+\boldsymbol{\mathrm{ny}}−\boldsymbol{\mathrm{my}}−\boldsymbol{\mathrm{ny}}} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{nx}}−\boldsymbol{\mathrm{my}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}}×\frac{\boldsymbol{\mathrm{xy}}+\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\boldsymbol{\mathrm{nx}}−\boldsymbol{\mathrm{my}}} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\frac{\boldsymbol{\mathrm{xy}}+\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}}=\frac{\boldsymbol{\mathrm{y}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}{\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)}=\frac{\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}} \\ $$$$\boldsymbol{\mathrm{klipto}}−\boldsymbol{\mathrm{quanta}} \\ $$
Answered by Spillover last updated on 05/Jul/24
 But y=x^e^x dy/dx=[e^x/x + ln(x)(e^x)](x^e^x) *dy/dx=(x^e^x)(e^x)[1/x + ln(x)]*](Q209248.png)
$$ \\ $$1) y=x^e^x Taking the natuaral logarithm of both sides we get ln(y)=ln(x^e^x) ln(y)=e^xln(x) Differentiating both sides with respect to x will imply that 1/y(dy/dx)=e^x(1/x) + ln(xy)(e^x) 1/y(dy/dx)=e^x/x +ln(x)(e^x) dy/dx=[e^x/x + ln(x)(e^x)](y) But y=x^e^x dy/dx=[e^x/x + ln(x)(e^x)](x^e^x) *dy/dx=(x^e^x)(e^x)[1/x + ln(x)]*
Commented by Tawa11 last updated on 05/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by Spillover last updated on 05/Jul/24
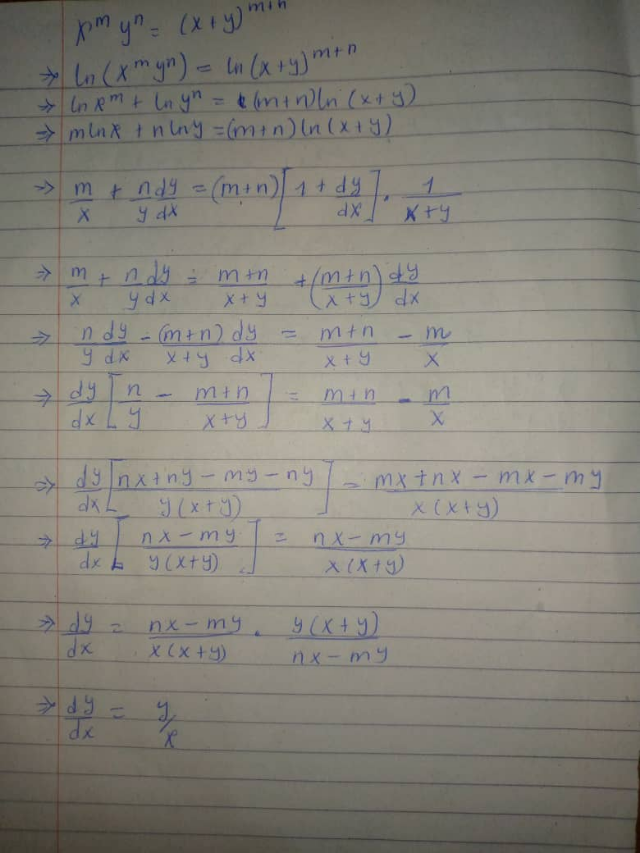
Commented by Tawa11 last updated on 05/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by Spillover last updated on 05/Jul/24
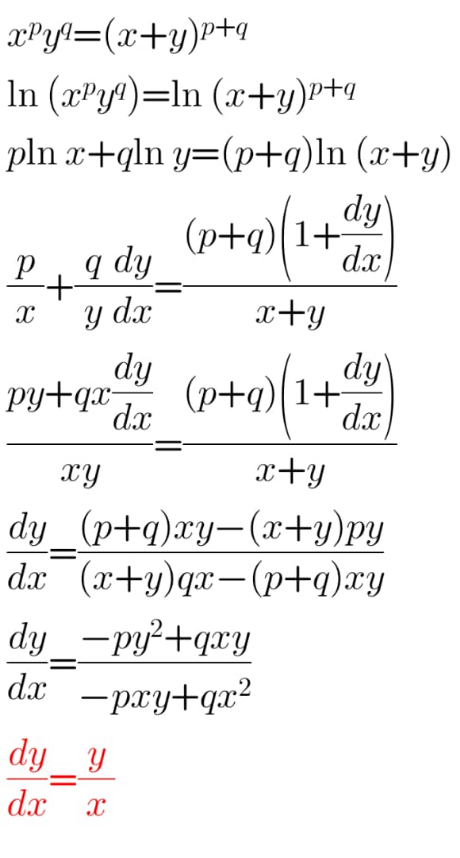
Commented by Tawa11 last updated on 05/Jul/24

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate} \\ $$
Answered by A5T last updated on 05/Jul/24
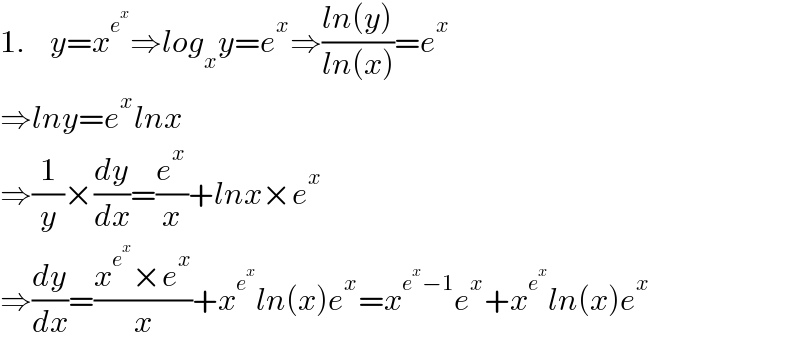
$$\mathrm{1}.\:\:\:\:{y}={x}^{{e}^{{x}} } \Rightarrow{log}_{{x}} {y}={e}^{{x}} \Rightarrow\frac{{ln}\left({y}\right)}{{ln}\left({x}\right)}={e}^{{x}} \\ $$$$\Rightarrow{lny}={e}^{{x}} {lnx} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}×\frac{{dy}}{{dx}}=\frac{{e}^{{x}} }{{x}}+{lnx}×{e}^{{x}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{{x}^{{e}^{{x}} } ×{e}^{{x}} }{{x}}+{x}^{{e}^{{x}} } {ln}\left({x}\right){e}^{{x}} ={x}^{{e}^{{x}} −\mathrm{1}} {e}^{{x}} +{x}^{{e}^{{x}} } {ln}\left({x}\right){e}^{{x}} \\ $$
Commented by Tawa11 last updated on 05/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Answered by A5T last updated on 05/Jul/24
![2. ln(x^m y^n )=ln[(x+y)^(m+n) ] ⇒mln(x)+nln(y)=(m+n)ln(x+y) (m/x)+(n/y)×(dy/dx)=((m+n)/(x+y))+((m+n)/(x+y))×(dy/dx) ⇒(dy/dx)((n/y)−((m+n)/(x+y)))=((m+n)/(x+y))−(m/x)=((nx−my)/(x(x+y))) ⇒(dy/dx)(((nx−my)/(y(x+y))))=((nx−my)/(x(x+y)))⇒(dy/dx)=(y/x)](Q209265.png)
$$\mathrm{2}.\:{ln}\left({x}^{{m}} {y}^{{n}} \right)={ln}\left[\left({x}+{y}\right)^{{m}+{n}} \right] \\ $$$$\Rightarrow{mln}\left({x}\right)+{nln}\left({y}\right)=\left({m}+{n}\right){ln}\left({x}+{y}\right) \\ $$$$\frac{{m}}{{x}}+\frac{{n}}{{y}}×\frac{{dy}}{{dx}}=\frac{{m}+{n}}{{x}+{y}}+\frac{{m}+{n}}{{x}+{y}}×\frac{{dy}}{{dx}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}\left(\frac{{n}}{{y}}−\frac{{m}+{n}}{{x}+{y}}\right)=\frac{{m}+{n}}{{x}+{y}}−\frac{{m}}{{x}}=\frac{{nx}−{my}}{{x}\left({x}+{y}\right)} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}\left(\frac{{nx}−{my}}{{y}\left({x}+{y}\right)}\right)=\frac{{nx}−{my}}{{x}\left({x}+{y}\right)}\Rightarrow\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$
Commented by Tawa11 last updated on 05/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Answered by lepuissantcedricjunior last updated on 05/Jul/24
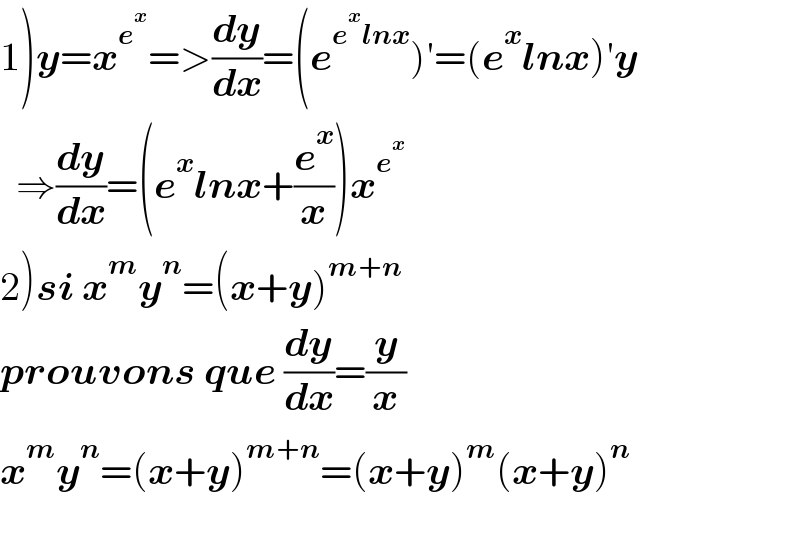
$$\left.\mathrm{1}\right)\boldsymbol{{y}}=\boldsymbol{{x}}^{\boldsymbol{{e}}^{\boldsymbol{{x}}} } =>\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\left(\boldsymbol{{e}}^{\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{lnx}}} \right)'=\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{lnx}}\right)'\boldsymbol{{y}} \\ $$$$\:\:\Rightarrow\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\left(\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{lnx}}+\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\boldsymbol{{x}}}\right)\boldsymbol{{x}}^{\boldsymbol{{e}}^{\boldsymbol{{x}}} } \\ $$$$\left.\mathrm{2}\right)\boldsymbol{{si}}\:\boldsymbol{{x}}^{\boldsymbol{{m}}} \boldsymbol{{y}}^{\boldsymbol{{n}}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\boldsymbol{{m}}+\boldsymbol{{n}}} \\ $$$$\boldsymbol{{prouvons}}\:\boldsymbol{{que}}\:\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\frac{\boldsymbol{{y}}}{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{x}}^{\boldsymbol{{m}}} \boldsymbol{{y}}^{\boldsymbol{{n}}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\boldsymbol{{m}}+\boldsymbol{{n}}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\boldsymbol{{m}}} \left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\boldsymbol{{n}}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 05/Jul/24
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
