
Question Number 209228 by universe last updated on 04/Jul/24
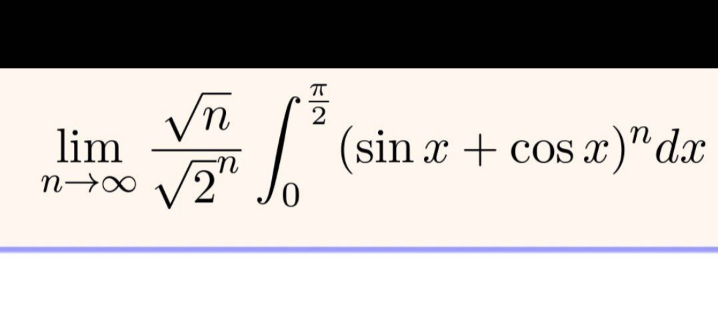
Answered by Frix last updated on 04/Jul/24
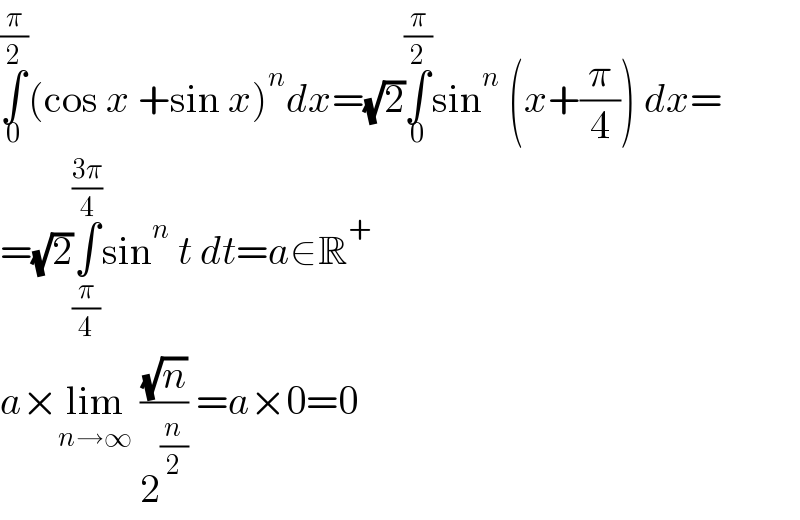
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\left(\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}\right)^{{n}} {dx}=\sqrt{\mathrm{2}}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{sin}^{{n}} \:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:{dx}= \\ $$$$=\sqrt{\mathrm{2}}\underset{\frac{\pi}{\mathrm{4}}} {\overset{\frac{\mathrm{3}\pi}{\mathrm{4}}} {\int}}\mathrm{sin}^{{n}} \:{t}\:{dt}={a}\in\mathbb{R}^{+} \\ $$$${a}×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{n}}}{\mathrm{2}^{\frac{{n}}{\mathrm{2}}} }\:={a}×\mathrm{0}=\mathrm{0} \\ $$
