Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 209223 by Tawa11 last updated on 04/Jul/24

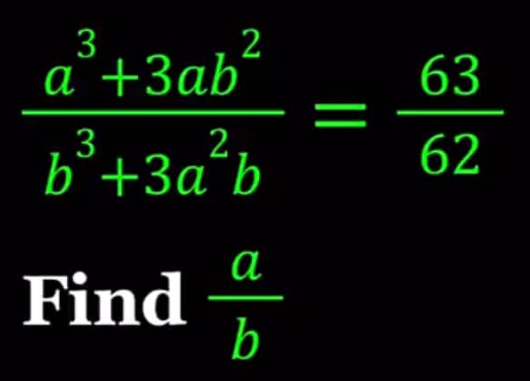
Answered by efronzo1 last updated on 04/Jul/24

((((a/b))^3 +3((a/b)))/(1+3((a/b))^2 )) = ((63)/(62)) (a/b) = x (x^3 +3x)62 = 63(1+3x^2 ) 62x^3 + 186x −189x^2 −63 = 0 (2x−3)(31x^2 −48x+21)=0 x ⇒ x = (a/b) = (3/2)

$$\:\:\: \\ $$$$ \frac{\left(\frac{{a}}{{b}}\right)^{\mathrm{3}} +\mathrm{3}\left(\frac{{a}}{{b}}\right)}{\mathrm{1}+\mathrm{3}\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{63}}{\mathrm{62}} \\ $$$$\:\: \frac{{a}}{{b}}\:=\:{x}\: \\ $$$$\:\:\:\left({x}^{\mathrm{3}} \:+\mathrm{3}{x}\right)\mathrm{62}\:=\:\mathrm{63}\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} \:\right) \\ $$$$\:\:\:\mathrm{62}{x}^{\mathrm{3}} \:+\:\mathrm{186}{x}\:−\mathrm{189}{x}^{\mathrm{2}} −\mathrm{63}\:=\:\mathrm{0} \\ $$$$\:\:\:\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{31}{x}^{\mathrm{2}} −\mathrm{48}{x}+\mathrm{21}\right)=\mathrm{0} \\ $$$$\:\:\: {x}\: \Rightarrow\:{x}\:=\:\frac{{a}}{{b}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\: \\ $$

Commented by Tawa11 last updated on 04/Jul/24

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Spillover last updated on 05/Jul/24

perfect

$${perfect} \\ $$

Answered by MATHEMATICSAM last updated on 04/Jul/24

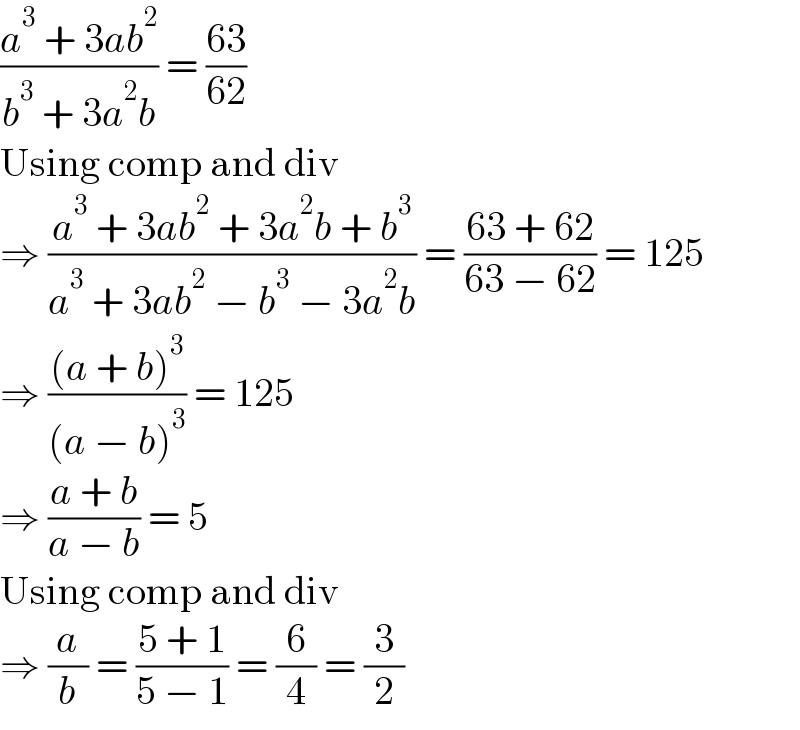
((a^3 + 3ab^2 )/(b^3 + 3a^2 b)) = ((63)/(62)) Using comp and div ⇒ ((a^3 + 3ab^2 + 3a^2 b + b^3 )/(a^3 + 3ab^2 − b^3 − 3a^2 b)) = ((63 + 62)/(63 − 62)) = 125 ⇒ (((a + b)^3 )/((a − b)^3 )) = 125 ⇒ ((a + b)/(a − b)) = 5 Using comp and div ⇒ (a/b) = ((5 + 1)/(5 − 1)) = (6/4) = (3/2)

$$\frac{{a}^{\mathrm{3}} \:+\:\mathrm{3}{ab}^{\mathrm{2}} }{{b}^{\mathrm{3}} \:+\:\mathrm{3}{a}^{\mathrm{2}} {b}}\:=\:\frac{\mathrm{63}}{\mathrm{62}} \\ $$$$\mathrm{Using}\:\mathrm{comp}\:\mathrm{and}\:\mathrm{div} \\ $$$$\Rightarrow\:\frac{{a}^{\mathrm{3}} \:+\:\mathrm{3}{ab}^{\mathrm{2}} \:+\:\mathrm{3}{a}^{\mathrm{2}} {b}\:+\:{b}^{\mathrm{3}} }{{a}^{\mathrm{3}} \:+\:\mathrm{3}{ab}^{\mathrm{2}} \:−\:{b}^{\mathrm{3}} \:−\:\mathrm{3}{a}^{\mathrm{2}} {b}}\:=\:\frac{\mathrm{63}\:+\:\mathrm{62}}{\mathrm{63}\:−\:\mathrm{62}}\:=\:\mathrm{125} \\ $$$$\Rightarrow\:\frac{\left({a}\:+\:{b}\right)^{\mathrm{3}} }{\left({a}\:−\:{b}\right)^{\mathrm{3}} }\:=\:\mathrm{125} \\ $$$$\Rightarrow\:\frac{{a}\:+\:{b}}{{a}\:−\:{b}}\:=\:\mathrm{5} \\ $$$$\mathrm{Using}\:\mathrm{comp}\:\mathrm{and}\:\mathrm{div} \\ $$$$\Rightarrow\:\frac{{a}}{{b}}\:=\:\frac{\mathrm{5}\:+\:\mathrm{1}}{\mathrm{5}\:−\:\mathrm{1}}\:=\:\frac{\mathrm{6}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 04/Jul/24

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com