Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

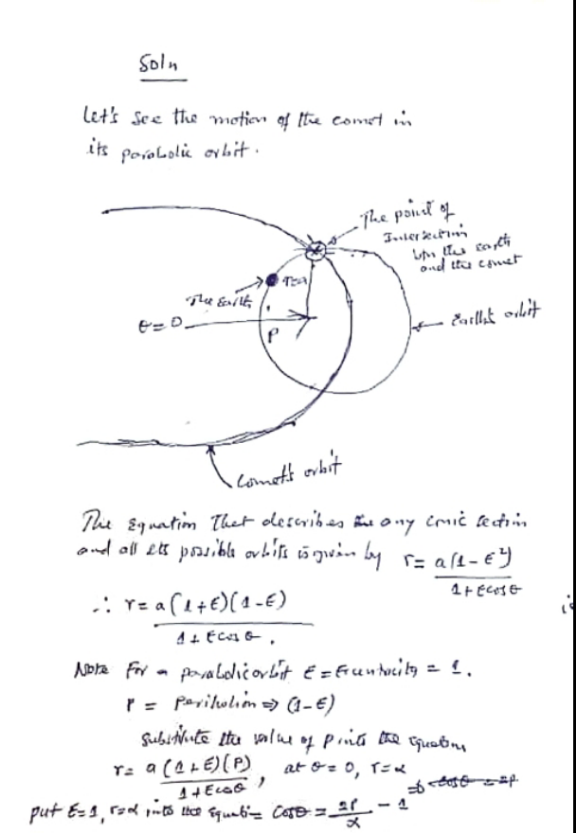
Question Number 209125 by Spillover last updated on 02/Jul/24

Answered by mr W last updated on 03/Jul/24

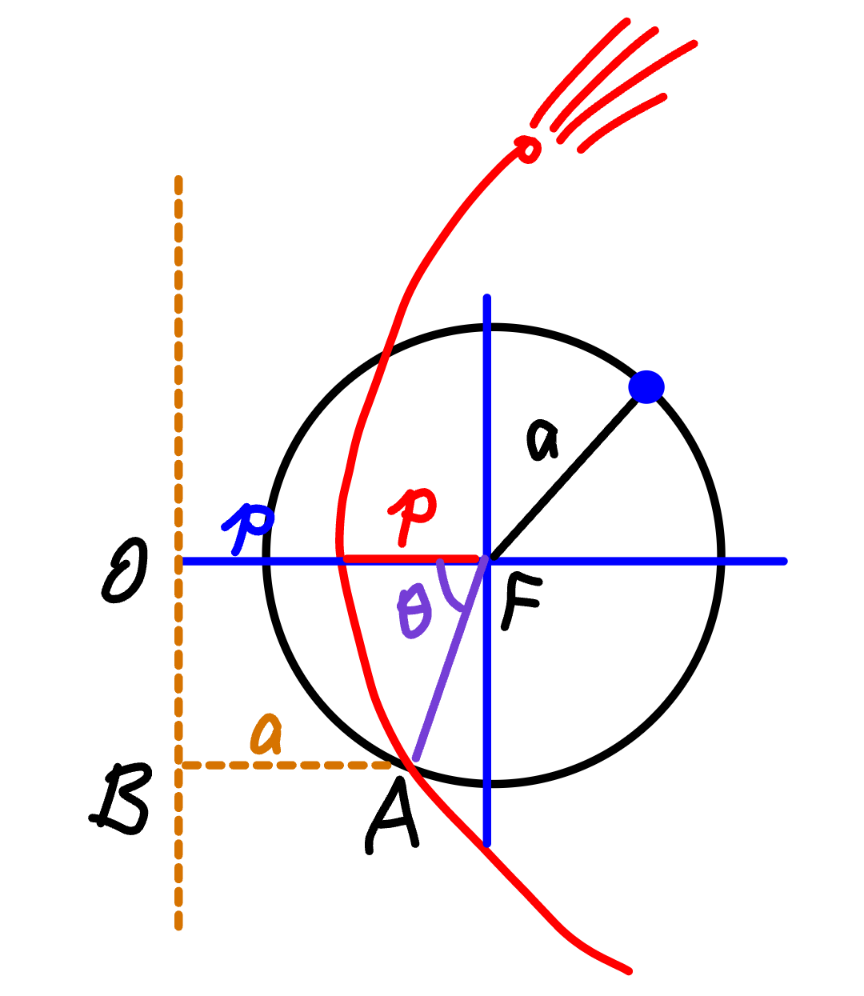
Commented by mr W last updated on 05/Jul/24

AB=AF=a a+a cos θ=2p ⇒cos θ=((2p)/a)−1

$${AB}={AF}={a} \\ $$$${a}+{a}\:\mathrm{cos}\:\theta=\mathrm{2}{p} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{2}{p}}{{a}}−\mathrm{1} \\ $$

Commented by Spillover last updated on 03/Jul/24

nice solution thank you

$${nice}\:{solution}\:{thank}\:{you} \\ $$

Commented by Spillover last updated on 03/Jul/24

Answered by Spillover last updated on 03/Jul/24

Commented by Spillover last updated on 04/Jul/24

thank you very for your clarification.

$${thank}\:{you}\:{very}\:{for}\:{your}\:{clarification}. \\ $$

Commented by mr W last updated on 03/Jul/24

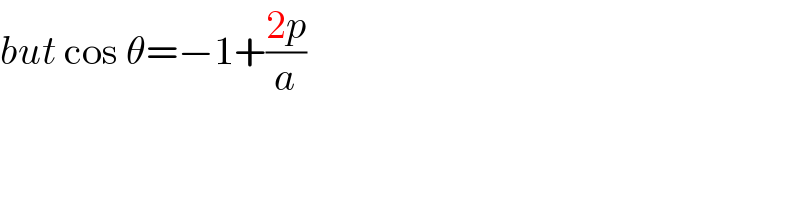
but cos θ=−1+((2p)/a)

$${but}\:\mathrm{cos}\:\theta=−\mathrm{1}+\frac{\mathrm{2}{p}}{{a}} \\ $$

Commented by Spillover last updated on 03/Jul/24

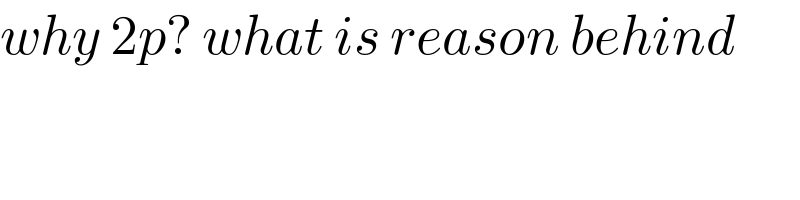
why 2p? what is reason behind

$${why}\:\mathrm{2}{p}?\:{what}\:{is}\:{reason}\:{behind} \\ $$

Commented by mr W last updated on 03/Jul/24

distance from focus to vertex is p distance from focus to directrix is 2p see also my diagram above.

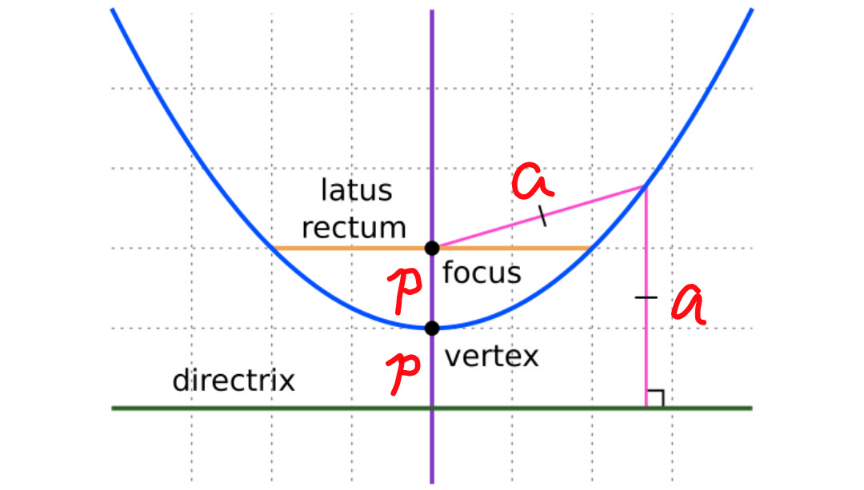
$${distance}\:{from}\:{focus}\:{to}\:{vertex}\:{is}\:{p} \\ $$$${distance}\:{from}\:{focus}\:{to}\:{directrix}\:{is}\:\mathrm{2}{p} \\ $$$${see}\:{also}\:{my}\:{diagram}\:{above}. \\ $$

Commented by mr W last updated on 03/Jul/24

Answered by Spillover last updated on 05/Jul/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com