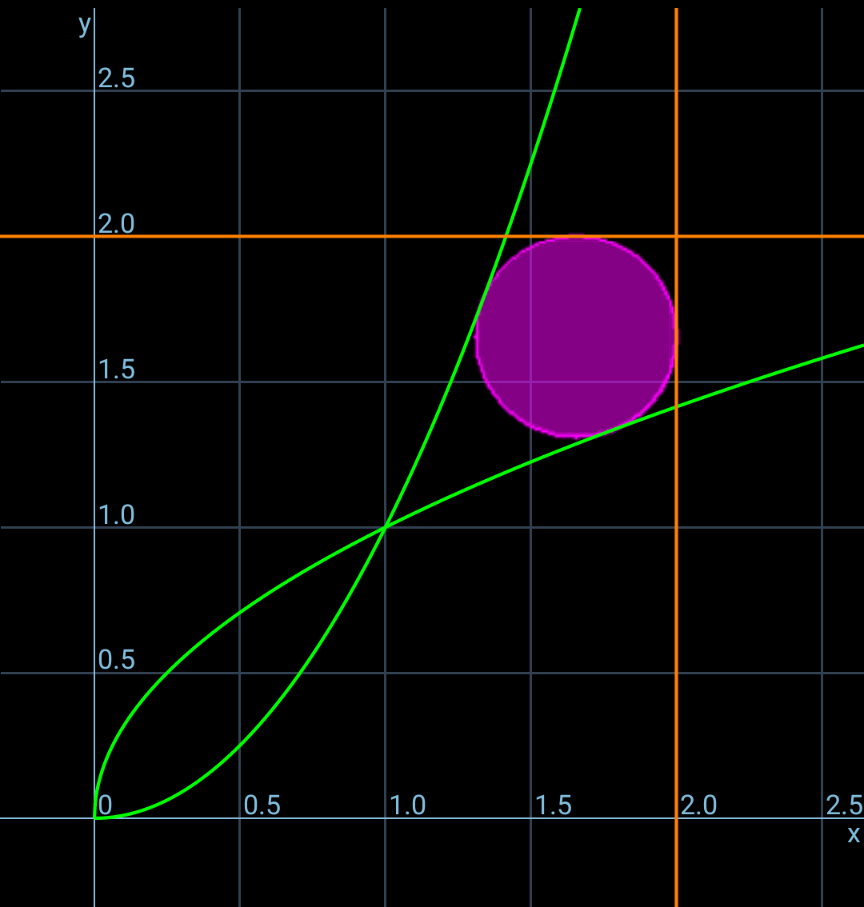
Question Number 209041 by alcohol last updated on 30/Jun/24
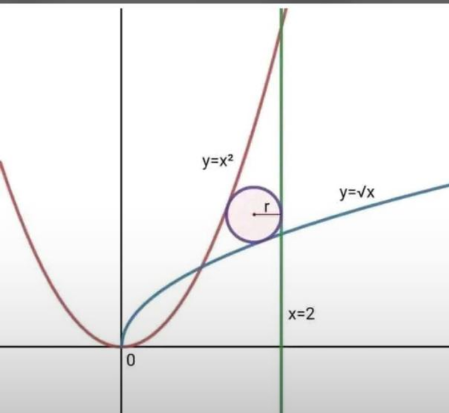
Commented by alcohol last updated on 30/Jun/24

$${find}\:{r} \\ $$
Commented by mr W last updated on 01/Jul/24
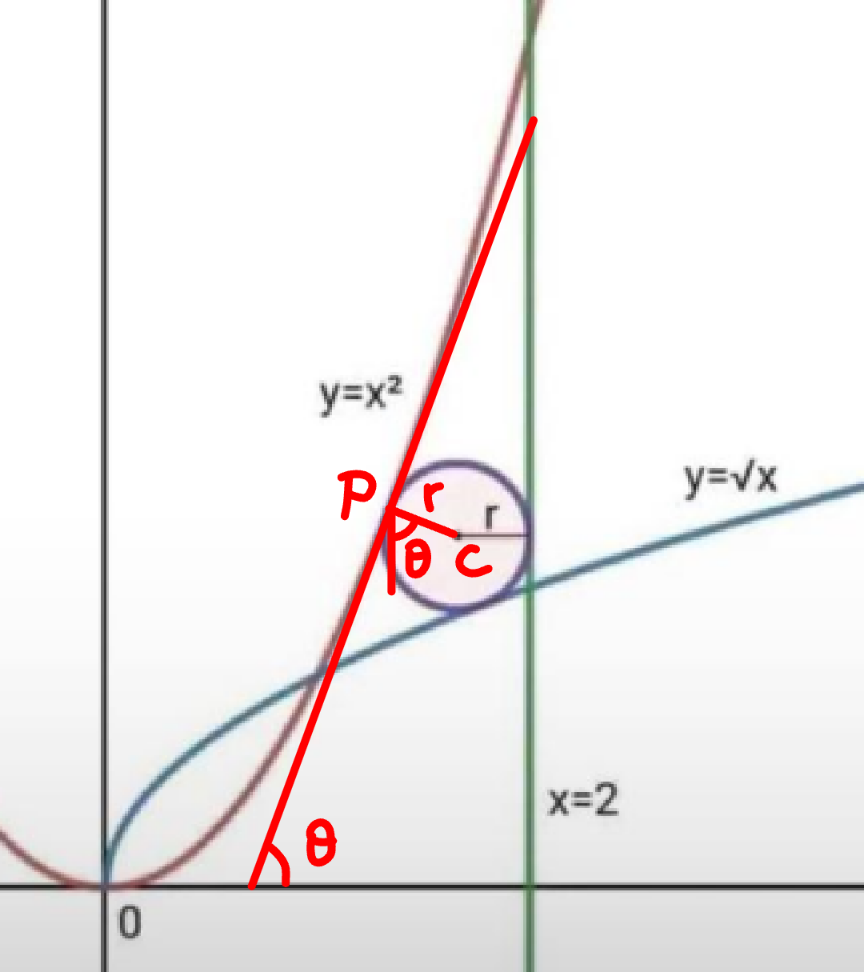
Answered by mr W last updated on 01/Jul/24
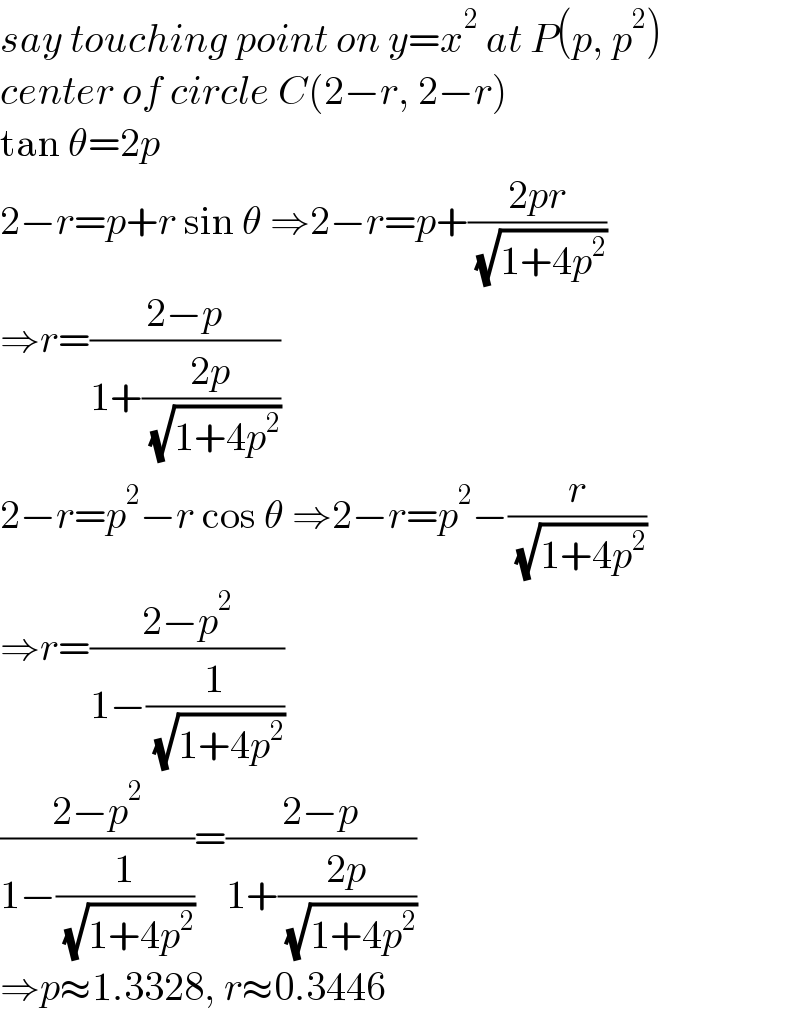
$${say}\:{touching}\:{point}\:{on}\:{y}={x}^{\mathrm{2}} \:{at}\:{P}\left({p},\:{p}^{\mathrm{2}} \right) \\ $$$${center}\:{of}\:{circle}\:{C}\left(\mathrm{2}−{r},\:\mathrm{2}−{r}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$$\mathrm{2}−{r}={p}+{r}\:\mathrm{sin}\:\theta\:\Rightarrow\mathrm{2}−{r}={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}−{p}}{\mathrm{1}+\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$$\mathrm{2}−{r}={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\theta\:\Rightarrow\mathrm{2}−{r}={p}^{\mathrm{2}} −\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}−{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$$\frac{\mathrm{2}−{p}^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}=\frac{\mathrm{2}−{p}}{\mathrm{1}+\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{p}\approx\mathrm{1}.\mathrm{3328},\:{r}\approx\mathrm{0}.\mathrm{3446} \\ $$
Commented by mr W last updated on 30/Jun/24