Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 209023 by Spillover last updated on 30/Jun/24

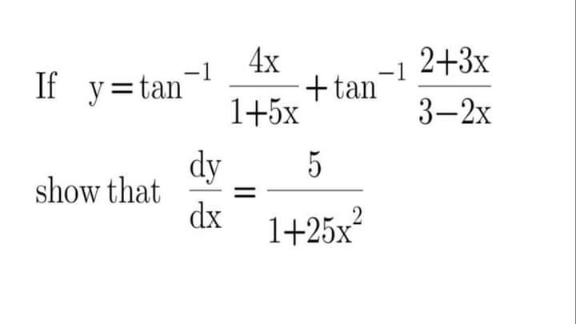
Commented by Spillover last updated on 01/Jul/24

let u=((4x)/(1+5x)) (du/dx)=(4/((1+5x)^2 )) (d/dx)(tan^(−1) ((4x)/(1+5x)))=((4/((1+5x)^2 ))/(1+(((4x)/(1+5x)))^2 ))=(4/(1+10x+25x^2 )) also (d/dx)(tan^(−1) ((2+3x)/(3−2x))) u=((2+3x)/(3−2x)) use qountient rule (du/dx)=((13+6x)/((3−2x)^2 )) (d/dx)(tan^(−1) ((2+3x)/(3−2x))) =((13+6x)/(13+13x^2 ))=((13+6x)/(13(1+x^2 ))) then =(4/(1+10x+25x^2 ))+((13+6x)/(13(1+x^2 ))) =(5/(1+25x^2 ))

$${let}\:{u}=\frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}}\:\:\:\:\:\:\frac{{du}}{{dx}}=\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{5}{x}\right)^{\mathrm{2}} } \\ $$$$\frac{{d}}{{dx}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}}\right)=\frac{\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{5}{x}\right)^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{1}+\mathrm{10}{x}+\mathrm{25}{x}^{\mathrm{2}} } \\ $$$${also} \\ $$$$\:\frac{{d}}{{dx}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}+\mathrm{3}{x}}{\mathrm{3}−\mathrm{2}{x}}\right)\:\:\:\:{u}=\frac{\mathrm{2}+\mathrm{3}{x}}{\mathrm{3}−\mathrm{2}{x}}\:\:\:\:\:{use}\:{qountient}\:{rule} \\ $$$$\frac{{du}}{{dx}}=\frac{\mathrm{13}+\mathrm{6}{x}}{\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{2}} }\:\: \\ $$$$\:\frac{{d}}{{dx}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}+\mathrm{3}{x}}{\mathrm{3}−\mathrm{2}{x}}\right)\:\:=\frac{\mathrm{13}+\mathrm{6}{x}}{\mathrm{13}+\mathrm{13}{x}^{\mathrm{2}} }=\frac{\mathrm{13}+\mathrm{6}{x}}{\mathrm{13}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${then}\: \\ $$$$=\frac{\mathrm{4}}{\mathrm{1}+\mathrm{10}{x}+\mathrm{25}{x}^{\mathrm{2}} }+\frac{\mathrm{13}+\mathrm{6}{x}}{\mathrm{13}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{5}}{\mathrm{1}+\mathrm{25}{x}^{\mathrm{2}} } \\ $$$$ \\ $$

Answered by A5T last updated on 30/Jun/24

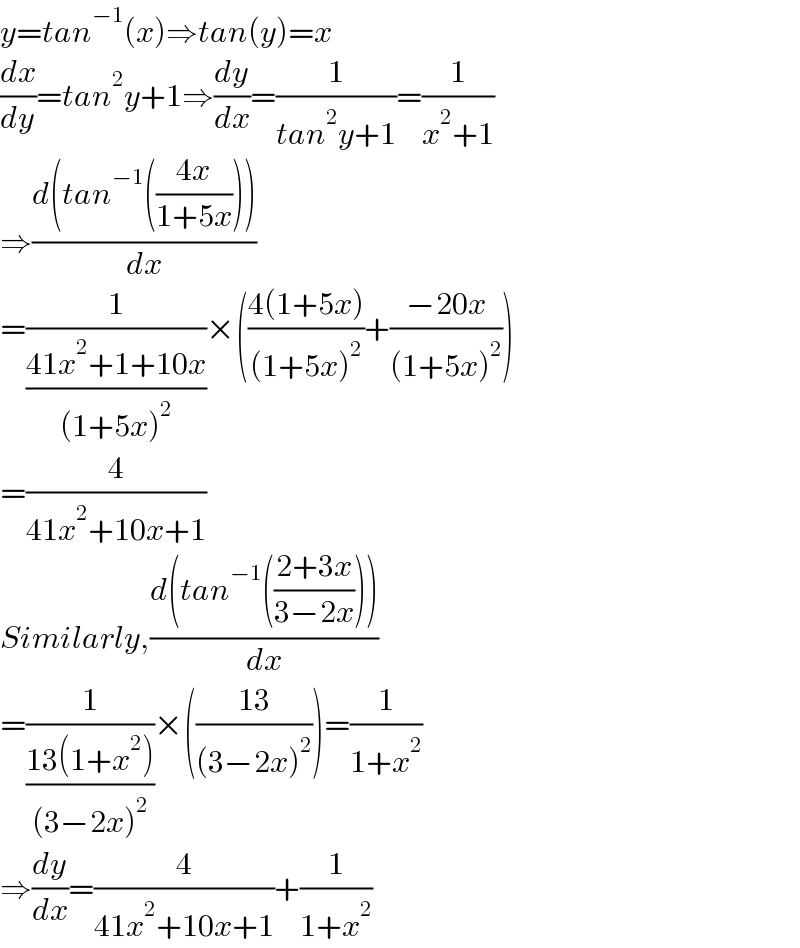
y=tan^(−1) (x)⇒tan(y)=x (dx/dy)=tan^2 y+1⇒(dy/dx)=(1/(tan^2 y+1))=(1/(x^2 +1)) ⇒((d(tan^(−1) (((4x)/(1+5x)))))/dx) =(1/((41x^2 +1+10x)/((1+5x)^2 )))×(((4(1+5x))/((1+5x)^2 ))+((−20x)/((1+5x)^2 ))) =(4/(41x^2 +10x+1)) Similarly,((d(tan^(−1) (((2+3x)/(3−2x)))))/dx) =(1/((13(1+x^2 ))/((3−2x)^2 )))×(((13)/((3−2x)^2 )))=(1/(1+x^2 )) ⇒(dy/dx)=(4/(41x^2 +10x+1))+(1/(1+x^2 ))

$${y}={tan}^{−\mathrm{1}} \left({x}\right)\Rightarrow{tan}\left({y}\right)={x} \\ $$$$\frac{{dx}}{{dy}}={tan}^{\mathrm{2}} {y}+\mathrm{1}\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {y}+\mathrm{1}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\frac{{d}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}}\right)\right)}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{41}{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{10}{x}}{\left(\mathrm{1}+\mathrm{5}{x}\right)^{\mathrm{2}} }}×\left(\frac{\mathrm{4}\left(\mathrm{1}+\mathrm{5}{x}\right)}{\left(\mathrm{1}+\mathrm{5}{x}\right)^{\mathrm{2}} }+\frac{−\mathrm{20}{x}}{\left(\mathrm{1}+\mathrm{5}{x}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{4}}{\mathrm{41}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{1}} \\ $$$${Similarly},\frac{{d}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}+\mathrm{3}{x}}{\mathrm{3}−\mathrm{2}{x}}\right)\right)}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{13}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{2}} }}×\left(\frac{\mathrm{13}}{\left(\mathrm{3}−\mathrm{2}{x}\right)^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{4}}{\mathrm{41}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$

Commented by Spillover last updated on 01/Jul/24

How did you get that 41?

$$ \\ $$How did you get that 41?

Commented by A5T last updated on 02/Jul/24

If y=tan^(−1) (x), then (dy/dx)=(1/(x^2 +1)) y=tan^(−1) [f(x)]⇒(dy/dx)=(1/([f(x)]^2 +1))×f′(x)

$${If}\:{y}={tan}^{−\mathrm{1}} \left({x}\right),\:{then}\:\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}={tan}^{−\mathrm{1}} \left[{f}\left({x}\right)\right]\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\mathrm{1}}×{f}'\left({x}\right) \\ $$

Answered by Spillover last updated on 01/Jul/24

Commented by A5T last updated on 01/Jul/24

This is not correct.

$${This}\:{is}\:{not}\:{correct}. \\ $$

Commented by Spillover last updated on 01/Jul/24

why?

$${why}? \\ $$

Commented by Spillover last updated on 01/Jul/24

recall tan^(−1) ((4x)/(1+5x))=tan^(−1) ((5x−x)/(1+5x))

$${recall}\: \\ $$$$\mathrm{tan}\:^{−\mathrm{1}} \frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}{x}−{x}}{\mathrm{1}+\mathrm{5}{x}} \\ $$$$ \\ $$

Commented by A5T last updated on 01/Jul/24

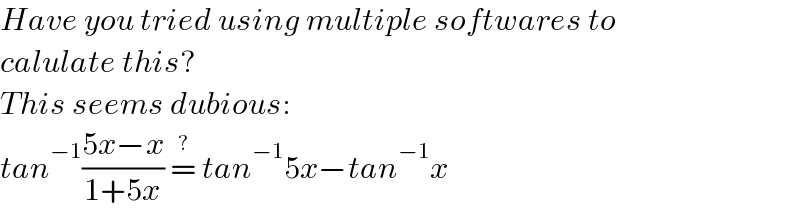
Have you tried using multiple softwares to calulate this? This seems dubious: tan^(−1) ((5x−x)/(1+5x)) =^? tan^(−1) 5x−tan^(−1) x

$${Have}\:{you}\:{tried}\:{using}\:{multiple}\:{softwares}\:{to} \\ $$$${calulate}\:{this}? \\ $$$${This}\:{seems}\:{dubious}:\: \\ $$$${tan}^{−\mathrm{1}} \frac{\mathrm{5}{x}−{x}}{\mathrm{1}+\mathrm{5}{x}}\:\overset{?} {=}\:{tan}^{−\mathrm{1}} \mathrm{5}{x}−{tan}^{−\mathrm{1}} {x} \\ $$

Commented by A5T last updated on 01/Jul/24

Commented by A5T last updated on 01/Jul/24

Commented by Spillover last updated on 01/Jul/24

Commented by A5T last updated on 01/Jul/24

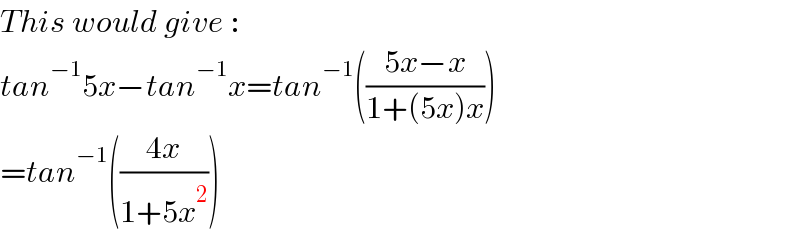
This would give : tan^(−1) 5x−tan^(−1) x=tan^(−1) (((5x−x)/(1+(5x)x))) =tan^(−1) (((4x)/(1+5x^2 )))

$${This}\:{would}\:{give}\:: \\ $$$${tan}^{−\mathrm{1}} \mathrm{5}{x}−{tan}^{−\mathrm{1}} {x}={tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}{x}−{x}}{\mathrm{1}+\left(\mathrm{5}{x}\right){x}}\right) \\ $$$$={tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}{x}}{\mathrm{1}+\mathrm{5}{x}^{\mathrm{2}} }\right) \\ $$

Commented by Spillover last updated on 02/Jul/24

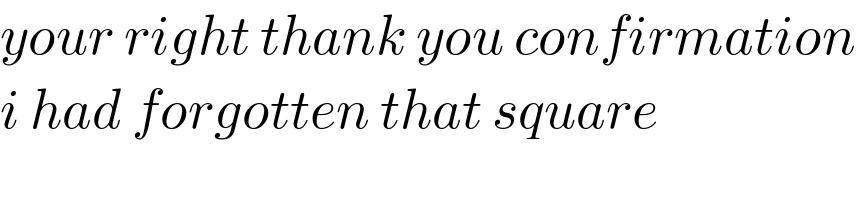
your right thank you confirmation i had forgotten that square

$${your}\:{right}\:{thank}\:{you}\:{confirmation} \\ $$$${i}\:{had}\:{forgotten}\:{that}\:{square} \\ $$

Commented by Spillover last updated on 02/Jul/24

now i understand you why my way is dubious

$${now}\:{i}\:{understand}\:{you}\:{why}\: \\ $$$${my}\:{way}\:{is}\:{dubious} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com