Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 208915 by Tawa11 last updated on 27/Jun/24

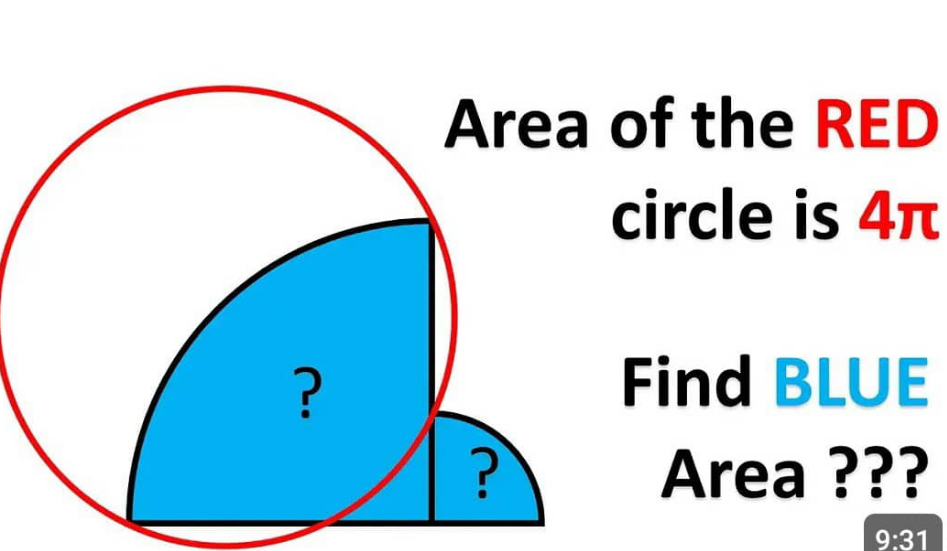
Answered by mr W last updated on 27/Jun/24

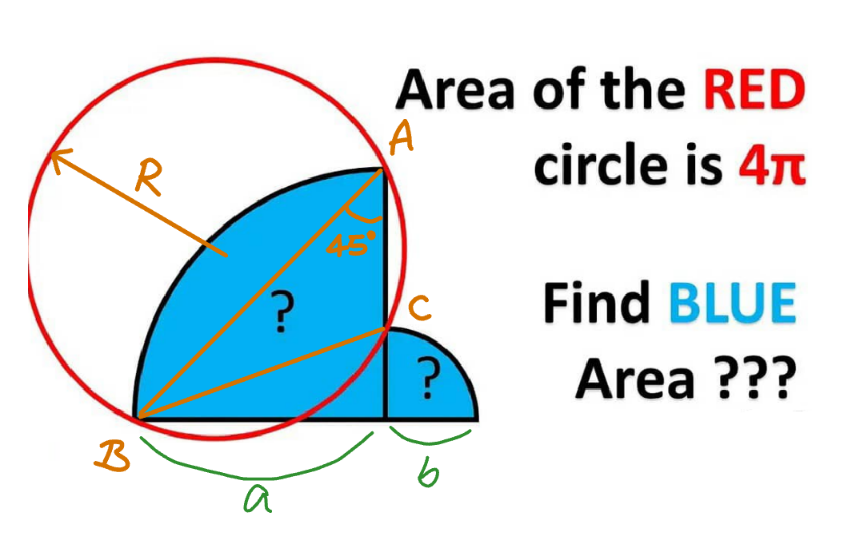
Commented by mr W last updated on 27/Jun/24

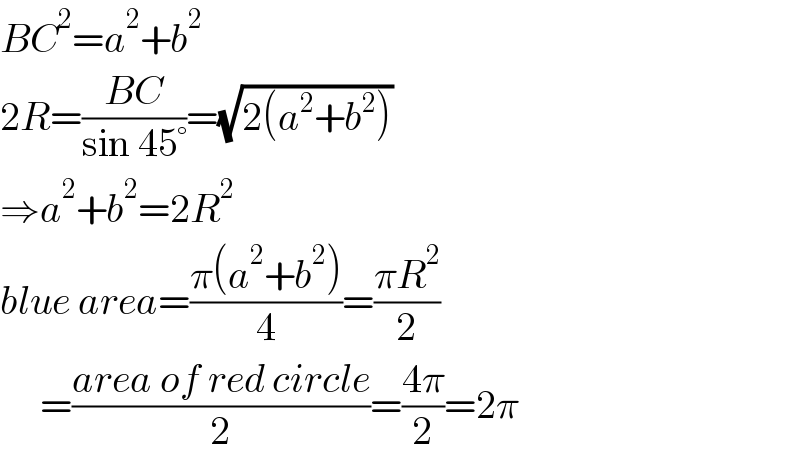
BC^2 =a^2 +b^2 2R=((BC)/(sin 45°))=(√(2(a^2 +b^2 ))) ⇒a^2 +b^2 =2R^2 blue area=((π(a^2 +b^2 ))/4)=((πR^2 )/2) =((area of red circle)/2)=((4π)/2)=2π

$${BC}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\mathrm{2}{R}=\frac{{BC}}{\mathrm{sin}\:\mathrm{45}°}=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \\ $$$${blue}\:{area}=\frac{\pi\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{\mathrm{4}}=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{{area}\:{of}\:{red}\:{circle}}{\mathrm{2}}=\frac{\mathrm{4}\pi}{\mathrm{2}}=\mathrm{2}\pi \\ $$

Commented by Tawa11 last updated on 27/Jun/24

Thanks sir. I appreciate sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com