
Question Number 208913 by efronzo1 last updated on 27/Jun/24
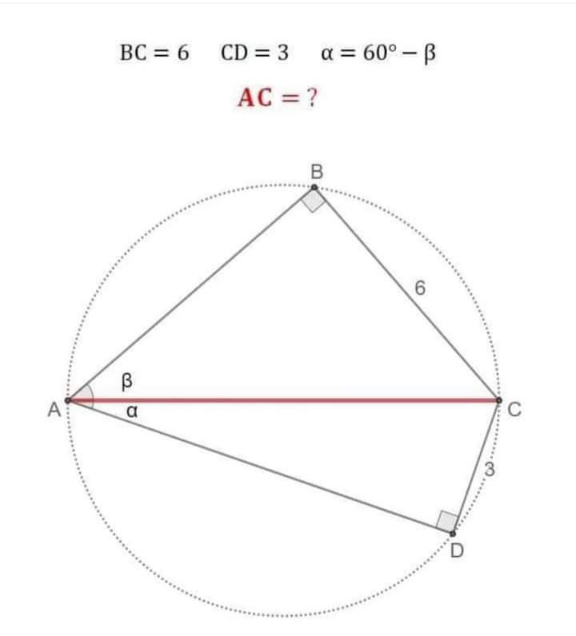
Answered by A5T last updated on 27/Jun/24
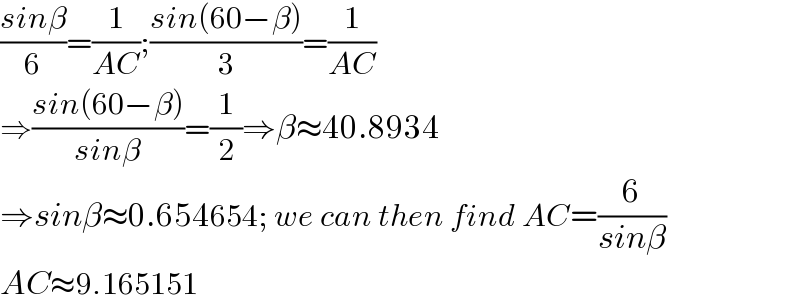
$$\frac{{sin}\beta}{\mathrm{6}}=\frac{\mathrm{1}}{{AC}};\frac{{sin}\left(\mathrm{60}−\beta\right)}{\mathrm{3}}=\frac{\mathrm{1}}{{AC}} \\ $$$$\Rightarrow\frac{{sin}\left(\mathrm{60}−\beta\right)}{{sin}\beta}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\beta\approx\mathrm{40}.\mathrm{8934} \\ $$$$\Rightarrow{sin}\beta\approx\mathrm{0}.\mathrm{654654};\:{we}\:{can}\:{then}\:{find}\:{AC}=\frac{\mathrm{6}}{{sin}\beta} \\ $$$${AC}\approx\mathrm{9}.\mathrm{165151} \\ $$
Answered by mr W last updated on 27/Jun/24
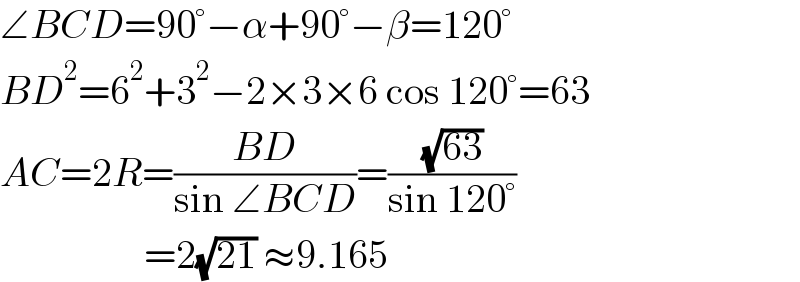
$$\angle{BCD}=\mathrm{90}°−\alpha+\mathrm{90}°−\beta=\mathrm{120}° \\ $$$${BD}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}×\mathrm{6}\:\mathrm{cos}\:\mathrm{120}°=\mathrm{63} \\ $$$${AC}=\mathrm{2}{R}=\frac{{BD}}{\mathrm{sin}\:\angle{BCD}}=\frac{\sqrt{\mathrm{63}}}{\mathrm{sin}\:\mathrm{120}°} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{21}}\:\approx\mathrm{9}.\mathrm{165} \\ $$
Answered by mr W last updated on 27/Jun/24
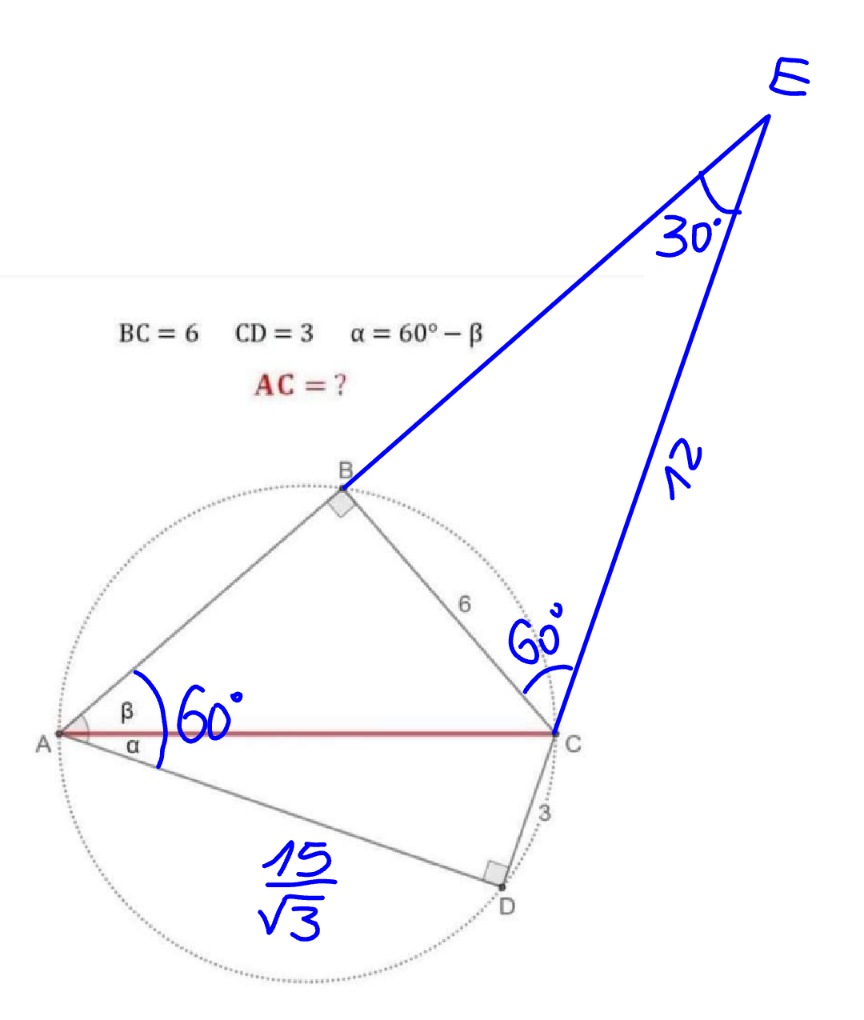
Commented by mr W last updated on 27/Jun/24
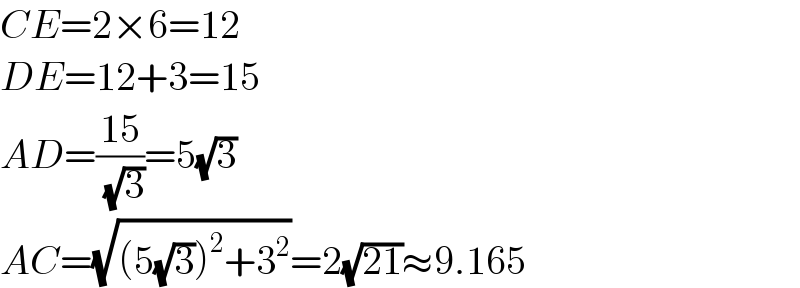
$${CE}=\mathrm{2}×\mathrm{6}=\mathrm{12} \\ $$$${DE}=\mathrm{12}+\mathrm{3}=\mathrm{15} \\ $$$${AD}=\frac{\mathrm{15}}{\:\sqrt{\mathrm{3}}}=\mathrm{5}\sqrt{\mathrm{3}} \\ $$$${AC}=\sqrt{\left(\mathrm{5}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{21}}\approx\mathrm{9}.\mathrm{165} \\ $$
Commented by Tawa11 last updated on 27/Jun/24

$$\mathrm{weldone}\:\mathrm{sirs} \\ $$
