Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 208896 by efronzo1 last updated on 26/Jun/24

Answered by MM42 last updated on 27/Jun/24

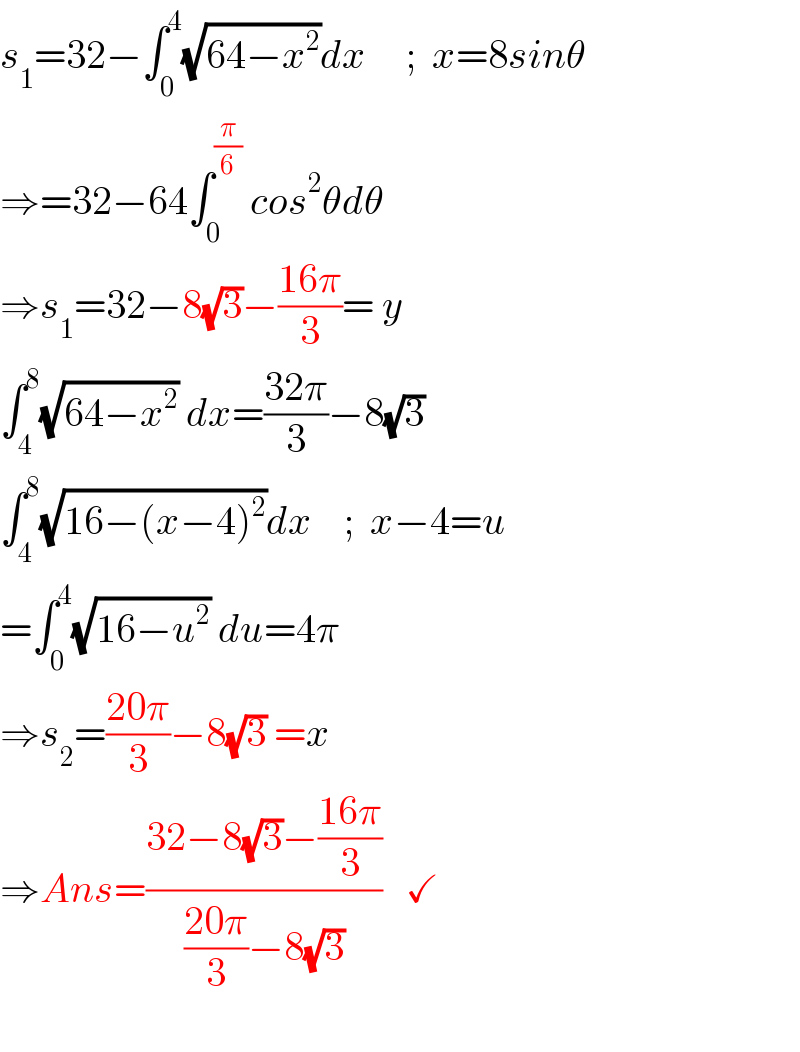
s_1 =32−∫_0 ^4 (√(64−x^2 ))dx ; x=8sinθ ⇒=32−64∫_0 ^(π/6) cos^2 θdθ ⇒s_1 =32−8(√3)−((16π)/3)= y ∫_4 ^8 (√(64−x^2 )) dx=((32π)/3)−8(√3) ∫_4 ^8 (√(16−(x−4)^2 ))dx ; x−4=u =∫_0 ^4 (√(16−u^2 )) du=4π ⇒s_2 =((20π)/3)−8(√3) =x ⇒Ans=((32−8(√3)−((16π)/3))/(((20π)/3)−8(√3))) ✓

$${s}_{\mathrm{1}} =\mathrm{32}−\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{64}−{x}^{\mathrm{2}} }{dx}\:\:\:\:\:;\:\:{x}=\mathrm{8}{sin}\theta \\ $$$$\Rightarrow=\mathrm{32}−\mathrm{64}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$\Rightarrow{s}_{\mathrm{1}} =\mathrm{32}−\mathrm{8}\sqrt{\mathrm{3}}−\frac{\mathrm{16}\pi}{\mathrm{3}}=\:{y} \\ $$$$\int_{\mathrm{4}} ^{\mathrm{8}} \sqrt{\mathrm{64}−{x}^{\mathrm{2}} }\:{dx}=\frac{\mathrm{32}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\int_{\mathrm{4}} ^{\mathrm{8}} \sqrt{\mathrm{16}−\left({x}−\mathrm{4}\right)^{\mathrm{2}} }{dx}\:\:\:\:;\:\:{x}−\mathrm{4}={u} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{16}−{u}^{\mathrm{2}} }\:{du}=\mathrm{4}\pi \\ $$$$\Rightarrow{s}_{\mathrm{2}} =\frac{\mathrm{20}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}}\:={x} \\ $$$$\Rightarrow{Ans}=\frac{\mathrm{32}−\mathrm{8}\sqrt{\mathrm{3}}−\frac{\mathrm{16}\pi}{\mathrm{3}}}{\frac{\mathrm{20}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}}}\:\:\:\checkmark \\ $$$$ \\ $$

Answered by mr W last updated on 26/Jun/24

big circle: y=(√(8^2 −x^2 )) small circle: y=(√(4^2 −(x−4)^2 ))=(√(8x−x^2 )) Y=∫_0 ^4 (8−(√(8^2 −x^2 )))dx=32−8(√3)−((16π)/3) X=∫_4 ^8 ((√(8^2 −x^2 ))−(√(8x−x^2 )))dx=((20π)/3)−8(√3) (Y/X)=((32−8(√3)−((16π)/3))/(((20π)/3)−8(√3)))≈0.196 or X=4×8−(8×8−((8^2 π)/4)−Y)−((4^2 π)/4) =−32+12π+32−8(√3)−((16π)/3) =((20π)/3)−8(√3)

$${big}\:{circle}: \\ $$$${y}=\sqrt{\mathrm{8}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${small}\:{circle}: \\ $$$${y}=\sqrt{\mathrm{4}^{\mathrm{2}} −\left({x}−\mathrm{4}\right)^{\mathrm{2}} }=\sqrt{\mathrm{8}{x}−{x}^{\mathrm{2}} } \\ $$$${Y}=\int_{\mathrm{0}} ^{\mathrm{4}} \left(\mathrm{8}−\sqrt{\mathrm{8}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right){dx}=\mathrm{32}−\mathrm{8}\sqrt{\mathrm{3}}−\frac{\mathrm{16}\pi}{\mathrm{3}} \\ $$$${X}=\int_{\mathrm{4}} ^{\mathrm{8}} \left(\sqrt{\mathrm{8}^{\mathrm{2}} −{x}^{\mathrm{2}} }−\sqrt{\mathrm{8}{x}−{x}^{\mathrm{2}} }\right){dx}=\frac{\mathrm{20}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\frac{{Y}}{{X}}=\frac{\mathrm{32}−\mathrm{8}\sqrt{\mathrm{3}}−\frac{\mathrm{16}\pi}{\mathrm{3}}}{\frac{\mathrm{20}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}}}\approx\mathrm{0}.\mathrm{196} \\ $$$${or} \\ $$$${X}=\mathrm{4}×\mathrm{8}−\left(\mathrm{8}×\mathrm{8}−\frac{\mathrm{8}^{\mathrm{2}} \pi}{\mathrm{4}}−{Y}\right)−\frac{\mathrm{4}^{\mathrm{2}} \pi}{\mathrm{4}} \\ $$$$\:\:\:\:=−\mathrm{32}+\mathrm{12}\pi+\mathrm{32}−\mathrm{8}\sqrt{\mathrm{3}}−\frac{\mathrm{16}\pi}{\mathrm{3}} \\ $$$$\:\:\:\:=\frac{\mathrm{20}\pi}{\mathrm{3}}−\mathrm{8}\sqrt{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com