
Question Number 208855 by efronzo1 last updated on 25/Jun/24

Answered by mr W last updated on 25/Jun/24
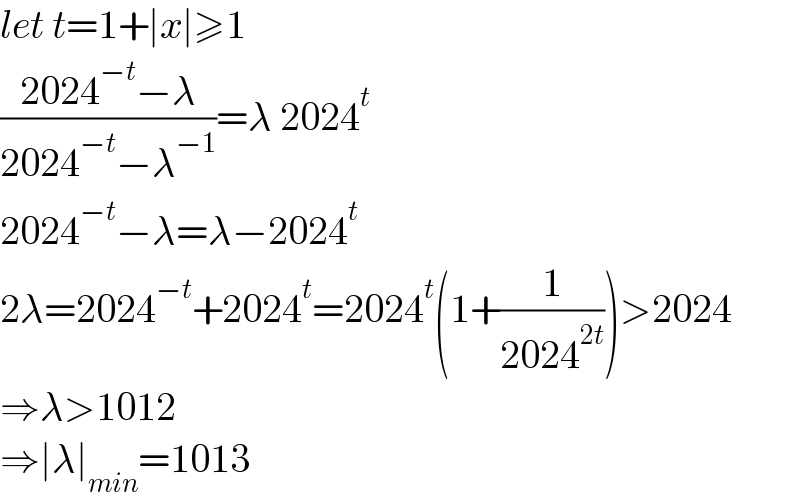
$${let}\:{t}=\mathrm{1}+\mid{x}\mid\geqslant\mathrm{1} \\ $$$$\frac{\mathrm{2024}^{−{t}} −\lambda}{\mathrm{2024}^{−{t}} −\lambda^{−\mathrm{1}} }=\lambda\:\mathrm{2024}^{{t}} \\ $$$$\mathrm{2024}^{−{t}} −\lambda=\lambda−\mathrm{2024}^{{t}} \\ $$$$\mathrm{2}\lambda=\mathrm{2024}^{−{t}} +\mathrm{2024}^{{t}} =\mathrm{2024}^{{t}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2024}^{\mathrm{2}{t}} }\right)>\mathrm{2024} \\ $$$$\Rightarrow\lambda>\mathrm{1012} \\ $$$$\Rightarrow\mid\lambda\mid_{{min}} =\mathrm{1013} \\ $$
