Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

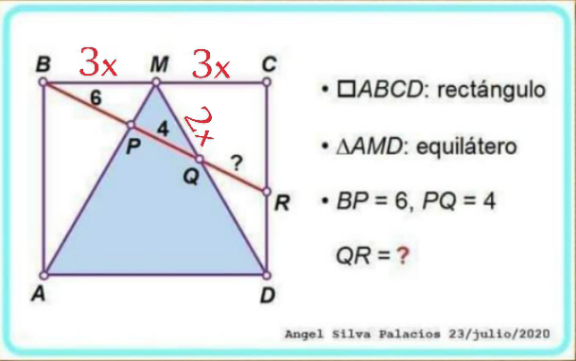
Question Number 208828 by efronzo1 last updated on 24/Jun/24

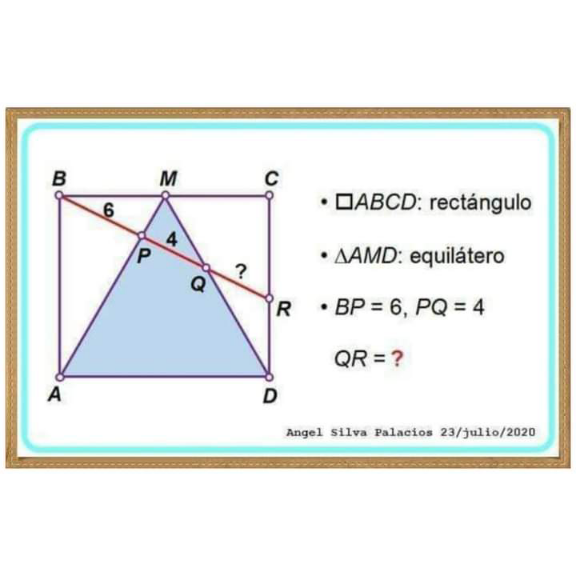
Answered by mr W last updated on 24/Jun/24

BM=MC=a, say AM=DM=2a ((BM)/6)=((MQ)/4) ⇒MQ=((2a)/3) ⇒QD=((4a)/3) (6+4)^2 =a^2 +(((2a)/3))^2 +a(((2a)/3)) ⇒a=((30)/( (√(19)))) ((sin ∠CBR)/((2a)/3))=((sin 120°)/(6+4)) sin ∠CBR=((√3)/(10×2))×(2/3)×((30)/( (√(19))))=((√3)/( (√(19)))) ((QR)/(sin 30°))=((QD)/(sin (90°+∠CBR)))=((4a)/(3 cos ∠CBR)) QR=((4×30)/(2×3(√(19))×(4/( (√(19))))))=5 ✓

$${BM}={MC}={a},\:{say} \\ $$$${AM}={DM}=\mathrm{2}{a} \\ $$$$\frac{{BM}}{\mathrm{6}}=\frac{{MQ}}{\mathrm{4}}\:\Rightarrow{MQ}=\frac{\mathrm{2}{a}}{\mathrm{3}}\:\Rightarrow{QD}=\frac{\mathrm{4}{a}}{\mathrm{3}} \\ $$$$\left(\mathrm{6}+\mathrm{4}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\frac{\mathrm{2}{a}}{\mathrm{3}}\right)^{\mathrm{2}} +{a}\left(\frac{\mathrm{2}{a}}{\mathrm{3}}\right) \\ $$$$\Rightarrow{a}=\frac{\mathrm{30}}{\:\sqrt{\mathrm{19}}} \\ $$$$\frac{\mathrm{sin}\:\angle{CBR}}{\frac{\mathrm{2}{a}}{\mathrm{3}}}=\frac{\mathrm{sin}\:\mathrm{120}°}{\mathrm{6}+\mathrm{4}} \\ $$$$\mathrm{sin}\:\angle{CBR}=\frac{\sqrt{\mathrm{3}}}{\mathrm{10}×\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{30}}{\:\sqrt{\mathrm{19}}}=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{19}}} \\ $$$$\frac{{QR}}{\mathrm{sin}\:\mathrm{30}°}=\frac{{QD}}{\mathrm{sin}\:\left(\mathrm{90}°+\angle{CBR}\right)}=\frac{\mathrm{4}{a}}{\mathrm{3}\:\mathrm{cos}\:\angle{CBR}} \\ $$$${QR}=\frac{\mathrm{4}×\mathrm{30}}{\mathrm{2}×\mathrm{3}\sqrt{\mathrm{19}}×\frac{\mathrm{4}}{\:\sqrt{\mathrm{19}}}}=\mathrm{5}\:\checkmark \\ $$

Commented by Tawa11 last updated on 24/Jun/24

Weldone sir. Learning.

$$\mathrm{Weldone}\:\mathrm{sir}.\:\mathrm{Learning}. \\ $$

Answered by A5T last updated on 24/Jun/24

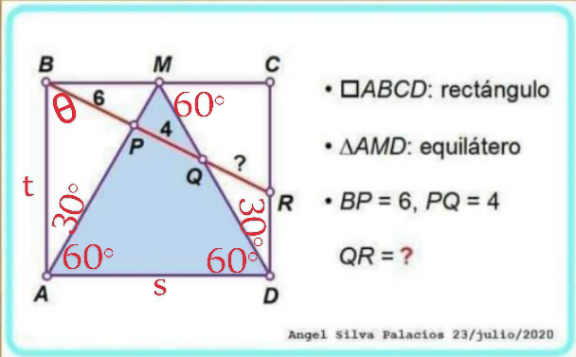
Commented by A5T last updated on 24/Jun/24

((BM)/(MC))×((CD)/(DR))×((RQ)/(QB))=1⇒1×(t/(DR))×(?/(10))=1...(i) tan30°=((s/2)/t)⇒s=((2t(√3))/3);((sinθ)/(AP))=((sin30°)/6)⇒AP=12sinθ ((sin60°)/6)=((sin(90−θ))/(MP))⇒MP=4(√3)cosθ MP+AP=((2t(√3))/3)=12sinθ+4(√3)cosθ...(ii) ((sin(90−θ))/(CR))=((sinθ)/s)⇒CR=scotθ=((2t(√3)cotθ)/3) ⇒DR=((3t−2t(√3)cotθ)/3); sinθ=((2t(√3))/(30+3?)) ⇒30sinθ+3?sinθ=2t(√3)⇒?=((2t(√3)−30sinθ)/(3sinθ)) (i)⇒(3/(3−2(√3)cotθ))×((2t(√3)−30sinθ)/(30sinθ))=1 ⇒t(√3)=30sinθ−10(√3)cosθ...(iii) (ii)&(iii)⇒tanθ=((4(√3))/3)⇒sinθ=(4/( (√(19))))⇒cosθ=((√3)/( (√(19)))) ⇒t=((30(√3))/( (√(19))))⇒?=((2t(√3)−30sinθ)/(3sinθ))=5

$$\frac{{BM}}{{MC}}×\frac{{CD}}{{DR}}×\frac{{RQ}}{{QB}}=\mathrm{1}\Rightarrow\mathrm{1}×\frac{{t}}{{DR}}×\frac{?}{\mathrm{10}}=\mathrm{1}...\left({i}\right) \\ $$$${tan}\mathrm{30}°=\frac{\frac{{s}}{\mathrm{2}}}{{t}}\Rightarrow{s}=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}}{\mathrm{3}};\frac{{sin}\theta}{{AP}}=\frac{{sin}\mathrm{30}°}{\mathrm{6}}\Rightarrow{AP}=\mathrm{12}{sin}\theta \\ $$$$\frac{{sin}\mathrm{60}°}{\mathrm{6}}=\frac{{sin}\left(\mathrm{90}−\theta\right)}{{MP}}\Rightarrow{MP}=\mathrm{4}\sqrt{\mathrm{3}}{cos}\theta \\ $$$${MP}+{AP}=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}}{\mathrm{3}}=\mathrm{12}{sin}\theta+\mathrm{4}\sqrt{\mathrm{3}}{cos}\theta...\left({ii}\right) \\ $$$$\frac{{sin}\left(\mathrm{90}−\theta\right)}{{CR}}=\frac{{sin}\theta}{{s}}\Rightarrow{CR}={scot}\theta=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}{cot}\theta}{\mathrm{3}} \\ $$$$\Rightarrow{DR}=\frac{\mathrm{3}{t}−\mathrm{2}{t}\sqrt{\mathrm{3}}{cot}\theta}{\mathrm{3}};\:{sin}\theta=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}}{\mathrm{30}+\mathrm{3}?} \\ $$$$\Rightarrow\mathrm{30}{sin}\theta+\mathrm{3}?{sin}\theta=\mathrm{2}{t}\sqrt{\mathrm{3}}\Rightarrow?=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}−\mathrm{30}{sin}\theta}{\mathrm{3}{sin}\theta} \\ $$$$\left({i}\right)\Rightarrow\frac{\mathrm{3}}{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}{cot}\theta}×\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}−\mathrm{30}{sin}\theta}{\mathrm{30}{sin}\theta}=\mathrm{1} \\ $$$$\Rightarrow{t}\sqrt{\mathrm{3}}=\mathrm{30}{sin}\theta−\mathrm{10}\sqrt{\mathrm{3}}{cos}\theta...\left({iii}\right) \\ $$$$\left({ii}\right)\&\left({iii}\right)\Rightarrow{tan}\theta=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\Rightarrow{sin}\theta=\frac{\mathrm{4}}{\:\sqrt{\mathrm{19}}}\Rightarrow{cos}\theta=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{19}}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{30}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{19}}}\Rightarrow?=\frac{\mathrm{2}{t}\sqrt{\mathrm{3}}−\mathrm{30}{sin}\theta}{\mathrm{3}{sin}\theta}=\mathrm{5} \\ $$

Answered by A5T last updated on 24/Jun/24

1×((CD)/(DR))×(?/(10))=1..(i)[△BCR with transversal MQD] ((BM)/6)=((MQ)/4)⇒BM=3x,MQ=2x ((DR)/(RC))×((6x)/(3x))×((2x)/(4x))=1⇒DR=RC[△MCD,trns.BQR] (i)⇒2×(?/(10))=1⇒?=((10)/2)=5

$$\mathrm{1}×\frac{{CD}}{{DR}}×\frac{?}{\mathrm{10}}=\mathrm{1}..\left({i}\right)\left[\bigtriangleup{BCR}\:{with}\:{transversal}\:{MQD}\right] \\ $$$$\frac{{BM}}{\mathrm{6}}=\frac{{MQ}}{\mathrm{4}}\Rightarrow{BM}=\mathrm{3}{x},{MQ}=\mathrm{2}{x} \\ $$$$\frac{{DR}}{{RC}}×\frac{\mathrm{6}{x}}{\mathrm{3}{x}}×\frac{\mathrm{2}{x}}{\mathrm{4}{x}}=\mathrm{1}\Rightarrow{DR}={RC}\left[\bigtriangleup{MCD},{trns}.{BQR}\right] \\ $$$$\left({i}\right)\Rightarrow\mathrm{2}×\frac{?}{\mathrm{10}}=\mathrm{1}\Rightarrow?=\frac{\mathrm{10}}{\mathrm{2}}=\mathrm{5} \\ $$

Commented by A5T last updated on 24/Jun/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com