Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 208743 by Tawa11 last updated on 22/Jun/24

Commented by Tawa11 last updated on 22/Jun/24

Area of red circle.

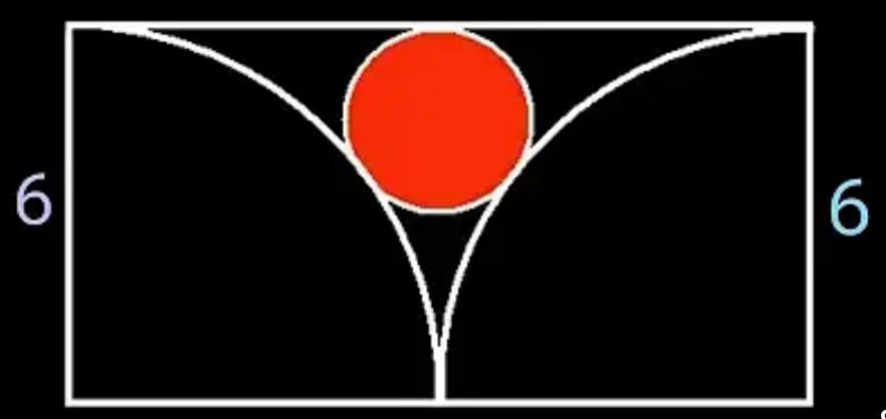
$$\mathrm{Area}\:\mathrm{of}\:\mathrm{red}\:\mathrm{circle}. \\ $$

Commented by Tawa11 last updated on 22/Jun/24

I got 1.5

$$\mathrm{I}\:\mathrm{got}\:\:\mathrm{1}.\mathrm{5} \\ $$

Commented by mr W last updated on 22/Jun/24

Commented by mr W last updated on 22/Jun/24

(1/( (√r)))=(2/( (√6))) ⇒r=(3/2)

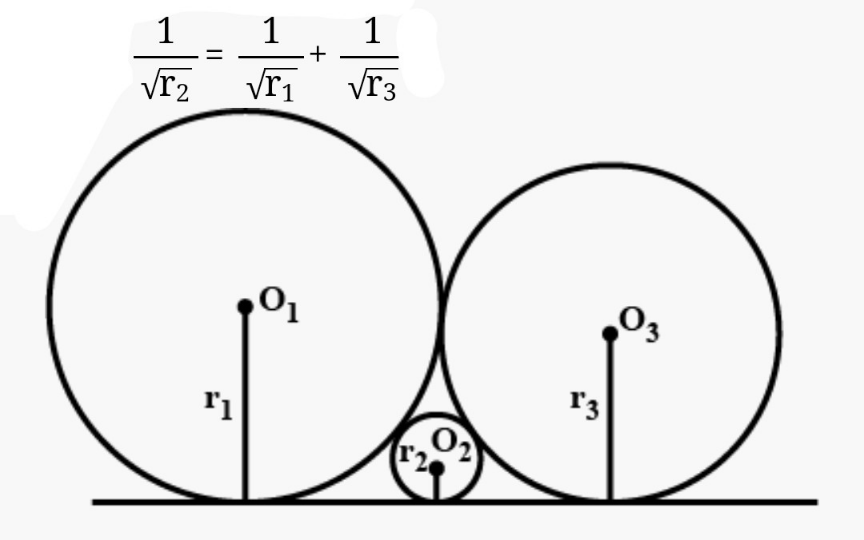
$$\frac{\mathrm{1}}{\:\sqrt{{r}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\:\Rightarrow{r}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 22/Jun/24

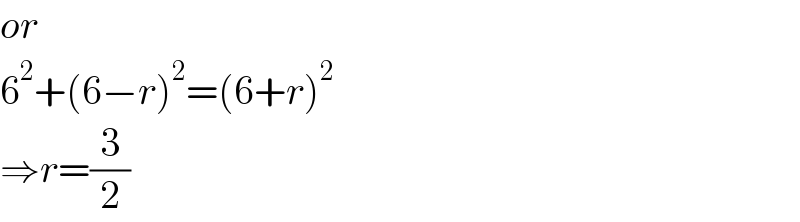
or 6^2 +(6−r)^2 =(6+r)^2 ⇒r=(3/2)

$${or} \\ $$$$\mathrm{6}^{\mathrm{2}} +\left(\mathrm{6}−{r}\right)^{\mathrm{2}} =\left(\mathrm{6}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 22/Jun/24

I used this. Based on what I learnt here

$$\mathrm{I}\:\mathrm{used}\:\mathrm{this}. \\ $$$$\mathrm{Based}\:\mathrm{on}\:\mathrm{what}\:\mathrm{I}\:\mathrm{learnt}\:\mathrm{here} \\ $$

Commented by Tawa11 last updated on 22/Jun/24

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 22/Jun/24

Sir please question 208741

$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{question}\:\mathrm{208741} \\ $$

Commented by Tawa11 last updated on 22/Jun/24

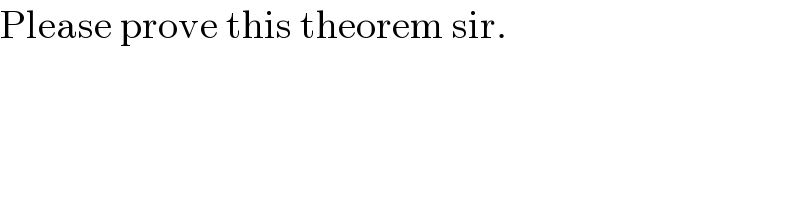
Please prove this theorem sir.

$$\mathrm{Please}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{theorem}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 22/Jun/24

https://en.m.wikipedia.org/wiki/Descartes%27_theorem

Answered by Sutrisno last updated on 22/Jun/24

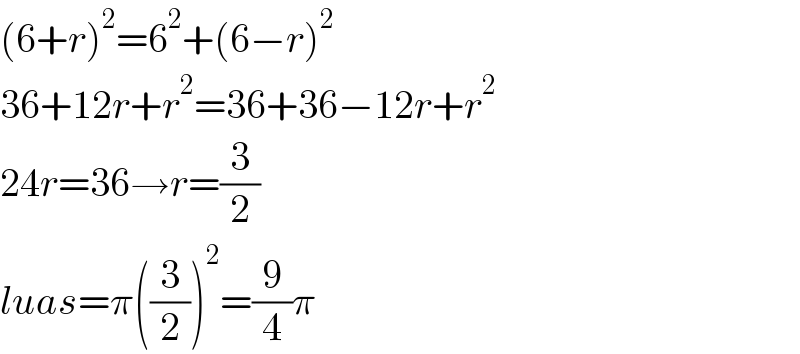
(6+r)^2 =6^2 +(6−r)^2 36+12r+r^2 =36+36−12r+r^2 24r=36→r=(3/2) luas=π((3/2))^2 =(9/4)π

$$\left(\mathrm{6}+{r}\right)^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +\left(\mathrm{6}−{r}\right)^{\mathrm{2}} \\ $$$$\mathrm{36}+\mathrm{12}{r}+{r}^{\mathrm{2}} =\mathrm{36}+\mathrm{36}−\mathrm{12}{r}+{r}^{\mathrm{2}} \\ $$$$\mathrm{24}{r}=\mathrm{36}\rightarrow{r}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${luas}=\pi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{4}}\pi \\ $$

Commented by Tawa11 last updated on 22/Jun/24

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com