Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

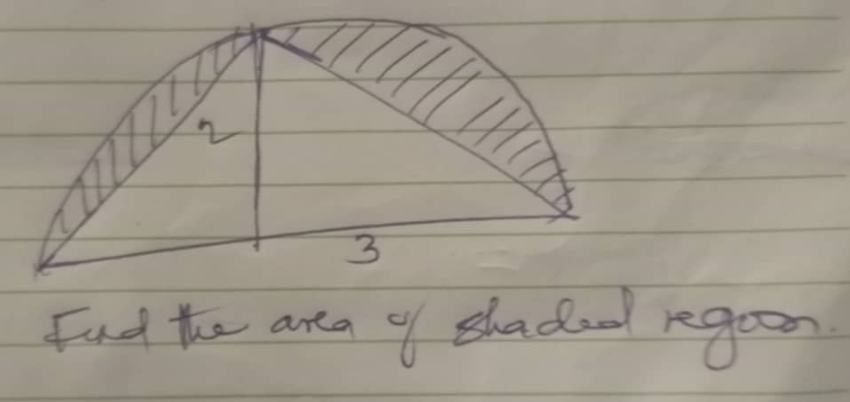
Question Number 208690 by Tawa11 last updated on 21/Jun/24

Answered by mr W last updated on 21/Jun/24

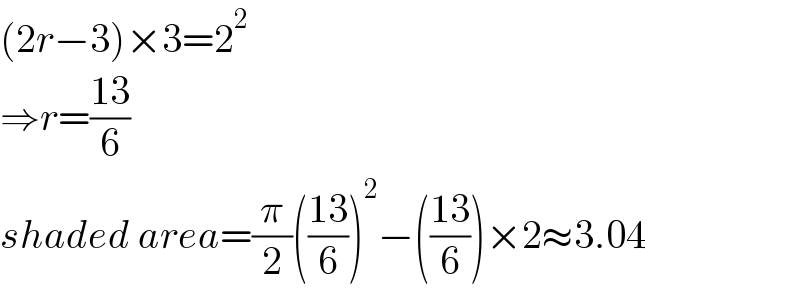
(2r−3)×3=2^2 ⇒r=((13)/6) shaded area=(π/2)(((13)/6))^2 −(((13)/6))×2≈3.04

$$\left(\mathrm{2}{r}−\mathrm{3}\right)×\mathrm{3}=\mathrm{2}^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$${shaded}\:{area}=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{13}}{\mathrm{6}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{13}}{\mathrm{6}}\right)×\mathrm{2}\approx\mathrm{3}.\mathrm{04} \\ $$

Commented by Tawa11 last updated on 21/Jun/24

Thanks sir. I really appreciate sir. But sir, You did this same approach in my previous question. I don′t understand the procedure. How: (2r − 3) × 3 = 2^2 You did: a^2 = (r − a)(r + a) in previous question. I think you did the same thing here too sir

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{sir}, \\ $$$$\mathrm{You}\:\mathrm{did}\:\mathrm{this}\:\mathrm{same}\:\mathrm{approach}\:\mathrm{in}\:\mathrm{my} \\ $$$$\mathrm{previous}\:\mathrm{question}. \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{procedure}. \\ $$$$ \\ $$$$\mathrm{How}:\:\:\:\left(\mathrm{2r}\:\:−\:\:\mathrm{3}\right)\:×\:\mathrm{3}\:\:=\:\:\mathrm{2}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{You}\:\mathrm{did}:\:\:\mathrm{a}^{\mathrm{2}} \:\:=\:\:\left(\mathrm{r}\:\:−\:\:\mathrm{a}\right)\left(\mathrm{r}\:\:+\:\:\mathrm{a}\right)\:\:\mathrm{in}\:\mathrm{previous}\:\mathrm{question}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{did}\:\mathrm{the}\:\mathrm{same}\:\mathrm{thing}\:\mathrm{here}\:\mathrm{too}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 21/Jun/24

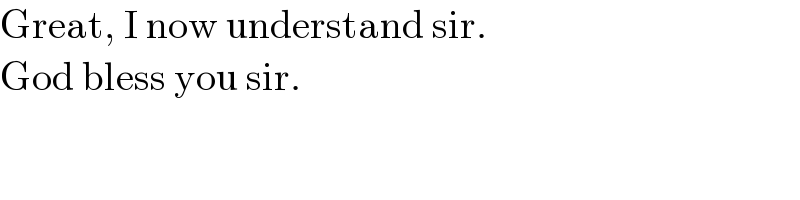
Great, I now understand sir. God bless you sir.

$$\mathrm{Great},\:\mathrm{I}\:\mathrm{now}\:\mathrm{understand}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 21/Jun/24

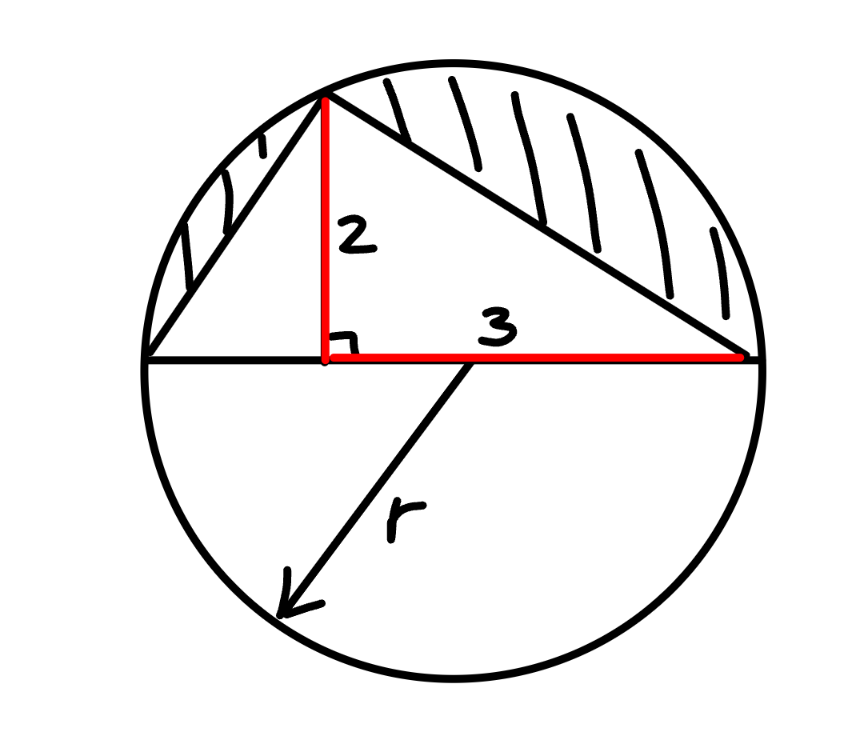
Commented by mr W last updated on 21/Jun/24

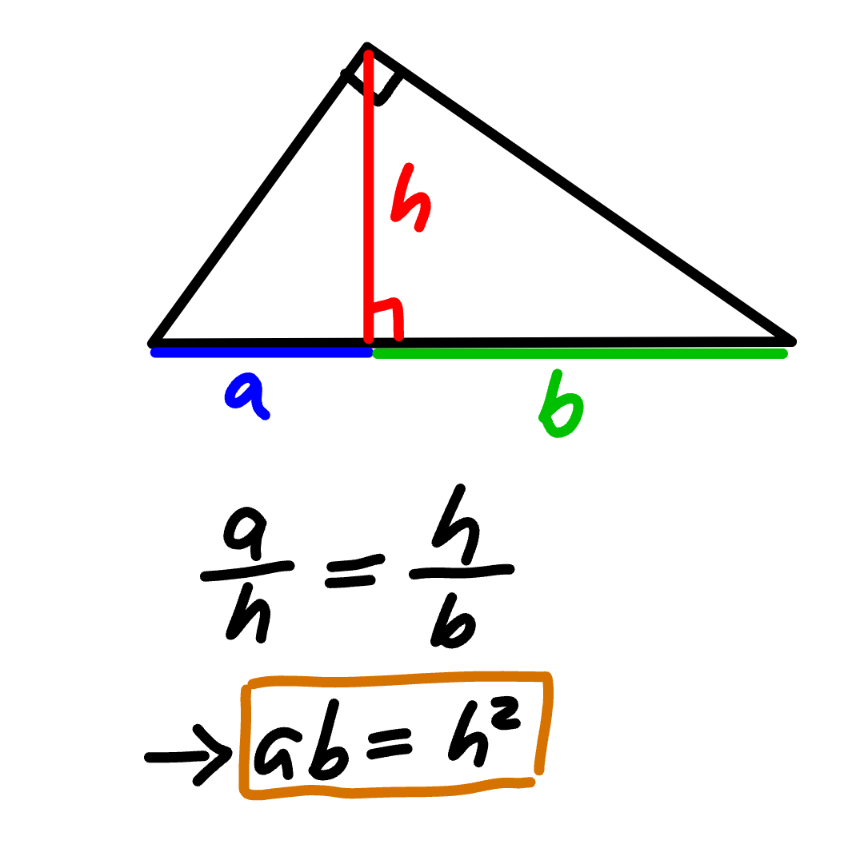
Commented by Tawa11 last updated on 21/Jun/24

Sir please see question 208467 if you have alternative approach sir.

$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{see}\:\mathrm{question}\:\mathrm{208467}\:\mathrm{if}\:\mathrm{you}\:\mathrm{have} \\ $$$$\mathrm{alternative}\:\mathrm{approach}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com