Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 208639 by Tawa11 last updated on 20/Jun/24

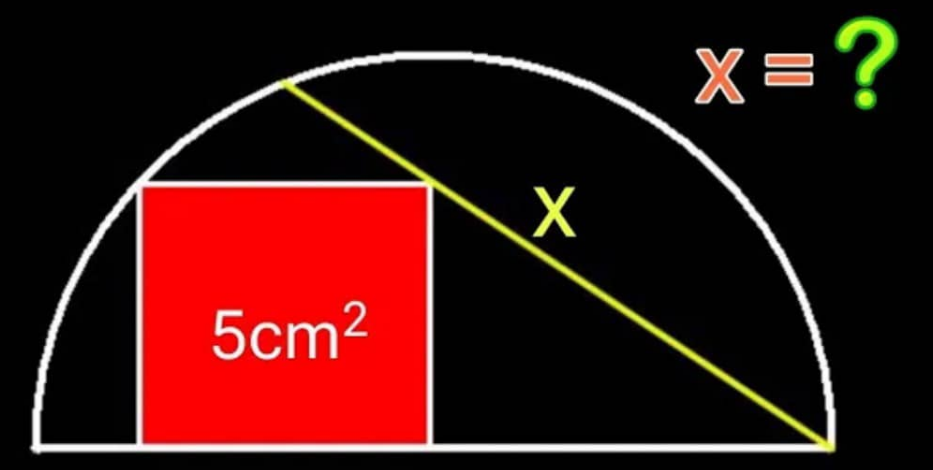
Commented by mr W last updated on 20/Jun/24

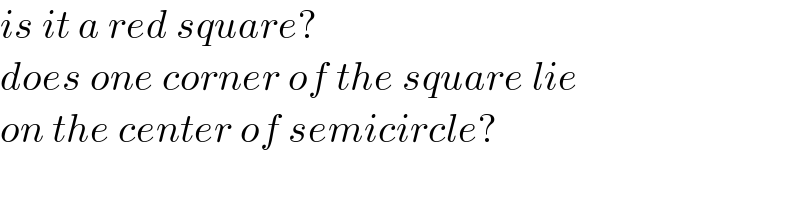
is it a red square? does one corner of the square lie on the center of semicircle?

$${is}\:{it}\:{a}\:{red}\:{square}? \\ $$$${does}\:{one}\:{corner}\:{of}\:{the}\:{square}\:{lie} \\ $$$${on}\:{the}\:{center}\:{of}\:{semicircle}? \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Yes sir.

$$\mathrm{Yes}\:\mathrm{sir}. \\ $$

Commented by som(math1967) last updated on 20/Jun/24

i got 4×(√(5/3))

$${i}\:{got}\:\mathrm{4}×\sqrt{\frac{\mathrm{5}}{\mathrm{3}}} \\ $$

Answered by AlagaIbile last updated on 20/Jun/24

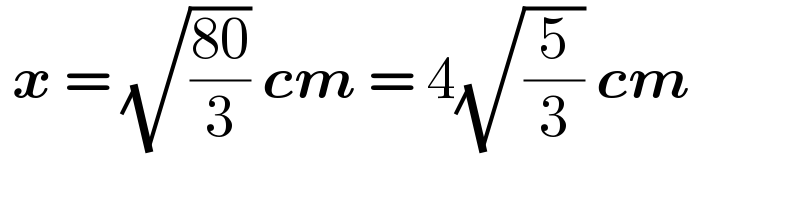
x = (√((80)/3)) cm = 4(√(5/3)) cm

$$\:\boldsymbol{{x}}\:=\:\sqrt{\frac{\mathrm{80}}{\mathrm{3}}}\:\boldsymbol{{cm}}\:=\:\mathrm{4}\sqrt{\frac{\mathrm{5}}{\mathrm{3}}}\:\boldsymbol{{cm}} \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 20/Jun/24

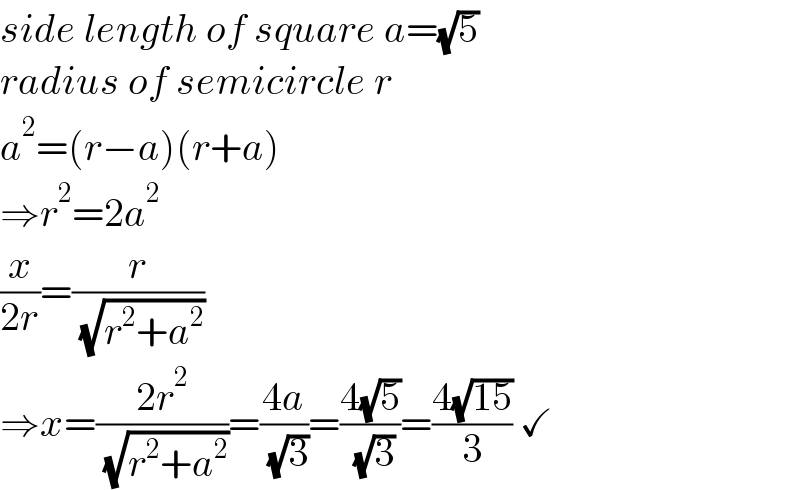
side length of square a=(√5) radius of semicircle r a^2 =(r−a)(r+a) ⇒r^2 =2a^2 (x/(2r))=(r/( (√(r^2 +a^2 )))) ⇒x=((2r^2 )/( (√(r^2 +a^2 ))))=((4a)/( (√3)))=((4(√5))/( (√3)))=((4(√(15)))/3) ✓

$${side}\:{length}\:{of}\:{square}\:{a}=\sqrt{\mathrm{5}} \\ $$$${radius}\:{of}\:{semicircle}\:{r} \\ $$$${a}^{\mathrm{2}} =\left({r}−{a}\right)\left({r}+{a}\right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} \\ $$$$\frac{{x}}{\mathrm{2}{r}}=\frac{{r}}{\:\sqrt{{r}^{\mathrm{2}} +{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{r}^{\mathrm{2}} }{\:\sqrt{{r}^{\mathrm{2}} +{a}^{\mathrm{2}} }}=\frac{\mathrm{4}{a}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\sqrt{\mathrm{15}}}{\mathrm{3}}\:\checkmark \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 20/Jun/24

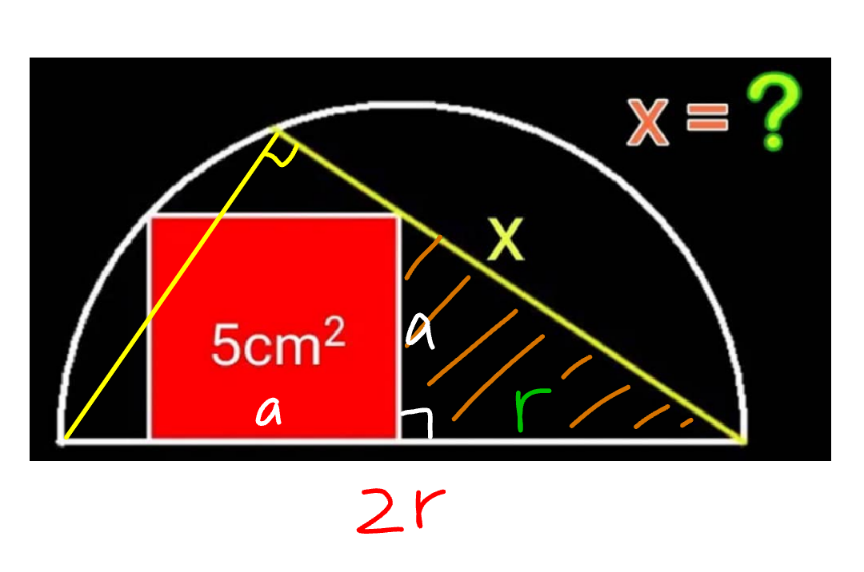
Commented by Tawa11 last updated on 20/Jun/24

Wow, I understand now sir.

$$\mathrm{Wow},\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{sir}. \\ $$

Answered by A5T last updated on 20/Jun/24

Commented by A5T last updated on 20/Jun/24

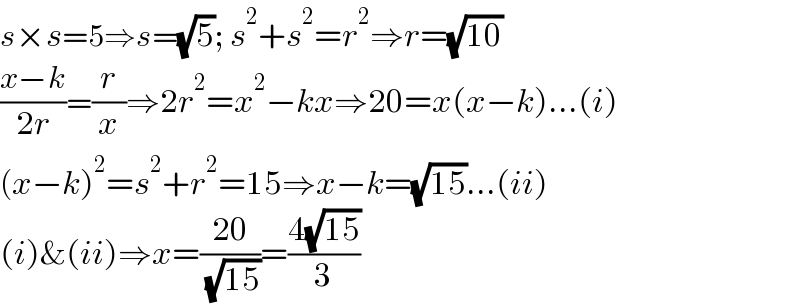
s×s=5⇒s=(√5); s^2 +s^2 =r^2 ⇒r=(√(10)) ((x−k)/(2r))=(r/x)⇒2r^2 =x^2 −kx⇒20=x(x−k)...(i) (x−k)^2 =s^2 +r^2 =15⇒x−k=(√(15))...(ii) (i)&(ii)⇒x=((20)/( (√(15))))=((4(√(15)))/3)

$${s}×{s}=\mathrm{5}\Rightarrow{s}=\sqrt{\mathrm{5}};\:{s}^{\mathrm{2}} +{s}^{\mathrm{2}} ={r}^{\mathrm{2}} \Rightarrow{r}=\sqrt{\mathrm{10}} \\ $$$$\frac{{x}−{k}}{\mathrm{2}{r}}=\frac{{r}}{{x}}\Rightarrow\mathrm{2}{r}^{\mathrm{2}} ={x}^{\mathrm{2}} −{kx}\Rightarrow\mathrm{20}={x}\left({x}−{k}\right)...\left({i}\right) \\ $$$$\left({x}−{k}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} +{r}^{\mathrm{2}} =\mathrm{15}\Rightarrow{x}−{k}=\sqrt{\mathrm{15}}...\left({ii}\right) \\ $$$$\left({i}\right)\&\left({ii}\right)\Rightarrow{x}=\frac{\mathrm{20}}{\:\sqrt{\mathrm{15}}}=\frac{\mathrm{4}\sqrt{\mathrm{15}}}{\mathrm{3}} \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Sir, am confused on. ((x − k)/(2r)) = (r/x) Please explain the rule that gives us that sir.

$$\mathrm{Sir},\:\mathrm{am}\:\mathrm{confused}\:\mathrm{on}. \\ $$$$\:\:\frac{\mathrm{x}\:\:−\:\:\mathrm{k}}{\mathrm{2r}}\:\:\:=\:\:\:\frac{\mathrm{r}}{\mathrm{x}} \\ $$$$\mathrm{Please}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{rule}\:\mathrm{that}\:\mathrm{gives}\:\mathrm{us}\:\mathrm{that}\:\mathrm{sir}. \\ $$

Commented by A5T last updated on 20/Jun/24

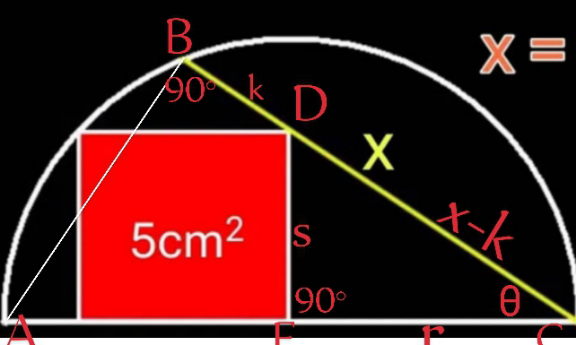
Commented by A5T last updated on 20/Jun/24

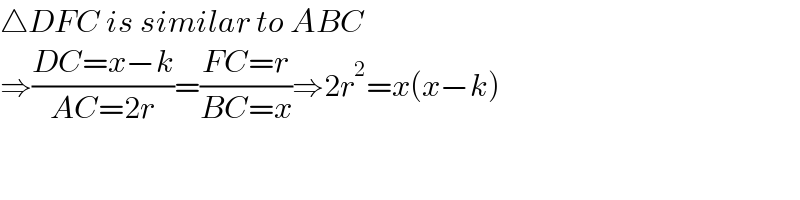
△DFC is similar to ABC ⇒((DC=x−k)/(AC=2r))=((FC=r)/(BC=x))⇒2r^2 =x(x−k)

$$\bigtriangleup{DFC}\:{is}\:{similar}\:{to}\:{ABC} \\ $$$$\Rightarrow\frac{{DC}={x}−{k}}{{AC}=\mathrm{2}{r}}=\frac{{FC}={r}}{{BC}={x}}\Rightarrow\mathrm{2}{r}^{\mathrm{2}} ={x}\left({x}−{k}\right) \\ $$

Commented by Tawa11 last updated on 20/Jun/24

Wow, I understand now sir

$$\mathrm{Wow},\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com