
Question and Answers Forum
Question Number 208553 by efronzo1 last updated on 18/Jun/24

Answered by Frix last updated on 18/Jun/24
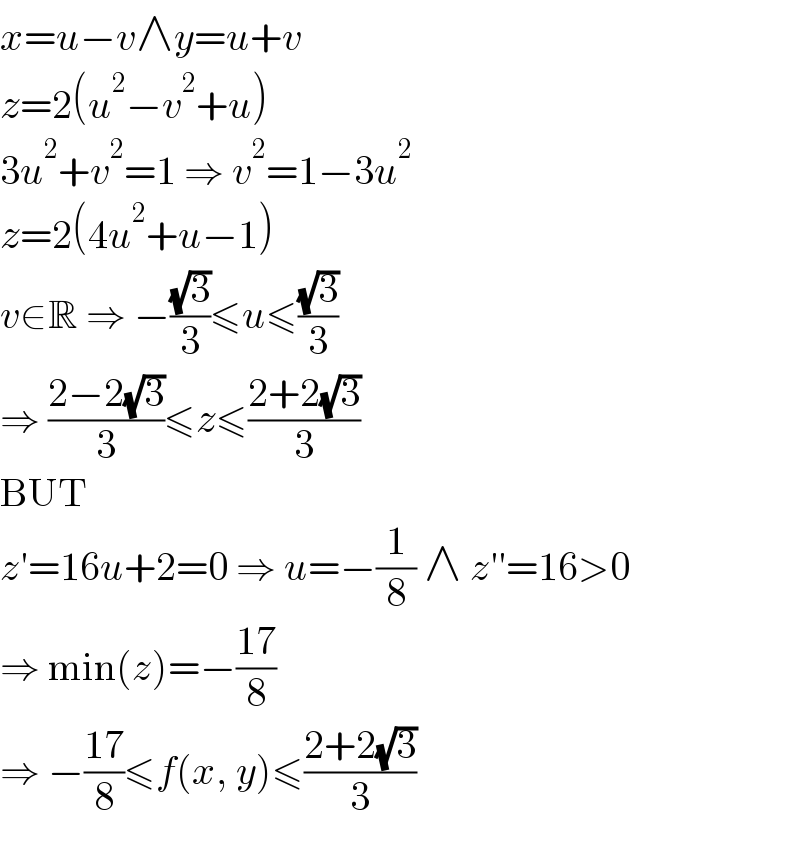
Commented by efronzo1 last updated on 18/Jun/24

Answered by A5T last updated on 18/Jun/24
![Suppose y=f(x) Then x^2 +y^2 +xy=1 ≡ x^2 +(f(x))^2 +xf(x)=1 (d/dx) of sides⇒2x+2f(x)f^′ (x)+xf^′ (x)+f(x)=0 ⇒f^′ (x)(2y+x)=−2x−y⇒f^′ (x)=((−2x−y)/(2y+x))...(i) Similarly,x+2xy+y=x+2xf(x)+f(x) (d/dx) of both sides⇒1+2xf′x+2f(x)+f^′ (x)=0 f^′ (x)=((−2y−1)/(2x+1))...(ii) (i)=(ii)⇒f^′ (x)=((−2y−1)/(2x+1))=((−2x−y)/(2y+x))[x≠((−1)/2),2y≠−x] ⇒4(x−y)(x+y)=−x+y=−(x−y) ⇒y=x or 4(x+y)=−1 y=x⇒3x^2 =1⇒x=+_− ((√3)/3)=y⇒f(x,y)=((2+_− (√3))/3) y=((−1)/4)−x⇒x=((+_− (√(61))−1)/8)⇒f(x,y)=((−17)/8) Comparing values⇒max(f(x,y))=((2+(√3))/3) and min(f(x,y))=((−17)/8)](Q208574.png)
Answered by efronzo1 last updated on 18/Jun/24

