Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 208540 by otchereabdullai@gmail.com last updated on 17/Jun/24

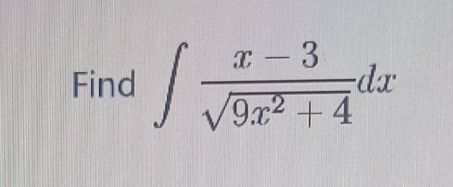
Answered by Sutrisno last updated on 18/Jun/24

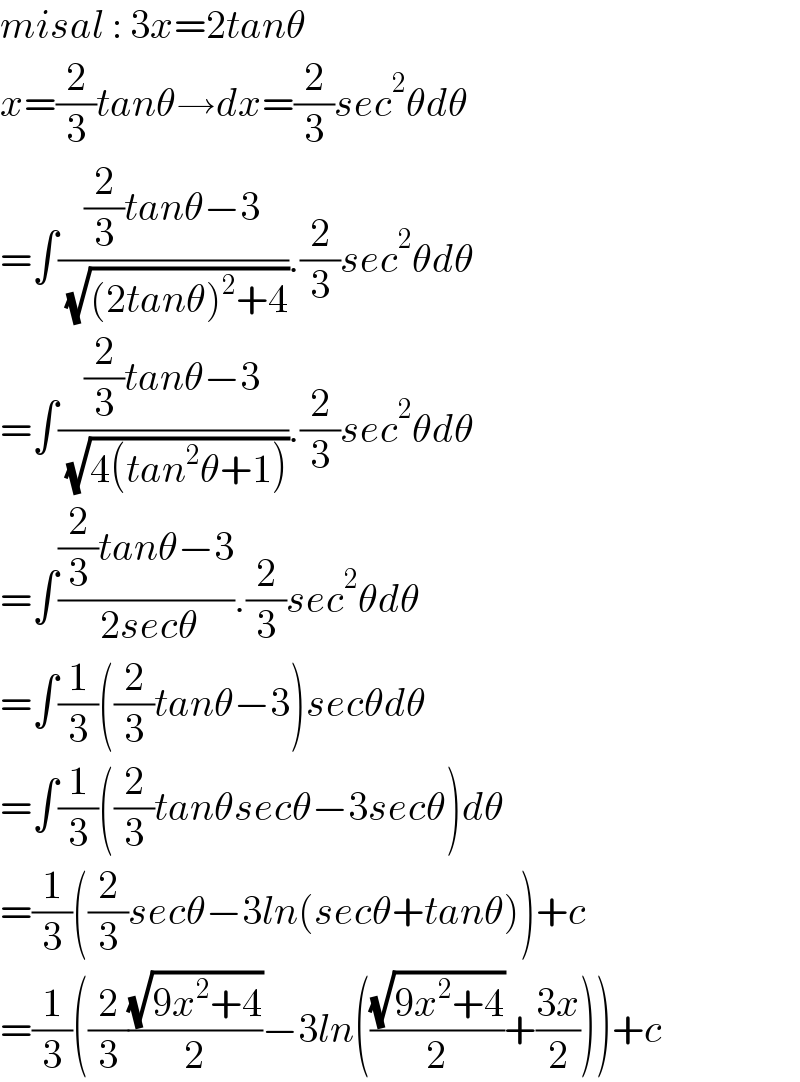
misal : 3x=2tanθ x=(2/3)tanθ→dx=(2/3)sec^2 θdθ =∫(((2/3)tanθ−3)/( (√((2tanθ)^2 +4)))).(2/3)sec^2 θdθ =∫(((2/3)tanθ−3)/( (√(4(tan^2 θ+1))))).(2/3)sec^2 θdθ =∫(((2/3)tanθ−3)/( 2secθ)).(2/3)sec^2 θdθ =∫(1/3)((2/3)tanθ−3)secθdθ =∫(1/3)((2/3)tanθsecθ−3secθ)dθ =(1/3)((2/3)secθ−3ln(secθ+tanθ))+c =(1/3)((2/3)((√(9x^2 +4))/2)−3ln(((√(9x^2 +4))/2)+((3x)/2)))+c

$${misal}\::\:\mathrm{3}{x}=\mathrm{2}{tan}\theta \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta\rightarrow{dx}=\frac{\mathrm{2}}{\mathrm{3}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int\frac{\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta−\mathrm{3}}{\:\sqrt{\left(\mathrm{2}{tan}\theta\right)^{\mathrm{2}} +\mathrm{4}}}.\frac{\mathrm{2}}{\mathrm{3}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int\frac{\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta−\mathrm{3}}{\:\sqrt{\mathrm{4}\left({tan}^{\mathrm{2}} \theta+\mathrm{1}\right)}}.\frac{\mathrm{2}}{\mathrm{3}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int\frac{\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta−\mathrm{3}}{\:\mathrm{2}{sec}\theta}.\frac{\mathrm{2}}{\mathrm{3}}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta−\mathrm{3}\right){sec}\theta{d}\theta \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}{tan}\theta{sec}\theta−\mathrm{3}{sec}\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}{sec}\theta−\mathrm{3}{ln}\left({sec}\theta+{tan}\theta\right)\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}−\mathrm{3}{ln}\left(\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{2}}+\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\right)+{c} \\ $$

Answered by Frix last updated on 18/Jun/24

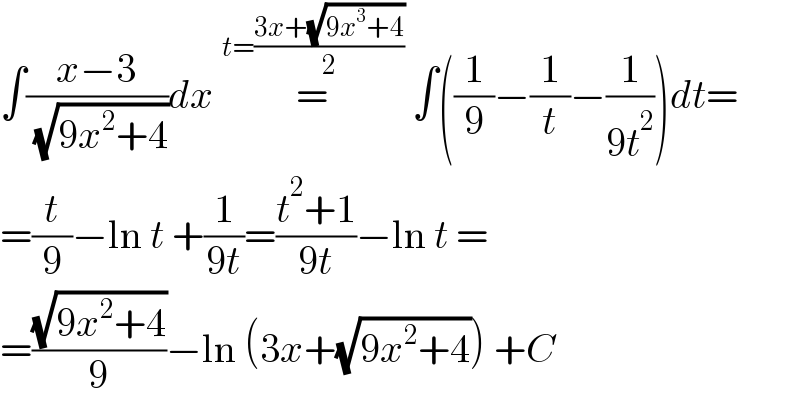
∫((x−3)/( (√(9x^2 +4))))dx =^(t=((3x+(√(9x^3 +4)))/2)) ∫((1/9)−(1/t)−(1/(9t^2 )))dt= =(t/9)−ln t +(1/(9t))=((t^2 +1)/(9t))−ln t = =((√(9x^2 +4))/9)−ln (3x+(√(9x^2 +4))) +C

$$\int\frac{{x}−\mathrm{3}}{\:\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}}}{dx}\:\overset{{t}=\frac{\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{3}} +\mathrm{4}}}{\mathrm{2}}} {=}\:\int\left(\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{9}{t}^{\mathrm{2}} }\right){dt}= \\ $$$$=\frac{{t}}{\mathrm{9}}−\mathrm{ln}\:{t}\:+\frac{\mathrm{1}}{\mathrm{9}{t}}=\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{9}{t}}−\mathrm{ln}\:{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}}}{\mathrm{9}}−\mathrm{ln}\:\left(\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{4}}\right)\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com