Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 208465 by Tawa11 last updated on 16/Jun/24

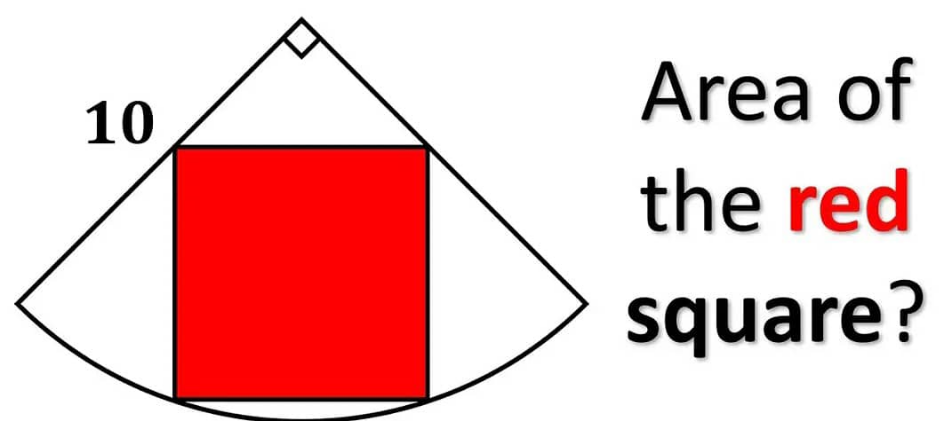
Answered by A5T last updated on 17/Jun/24

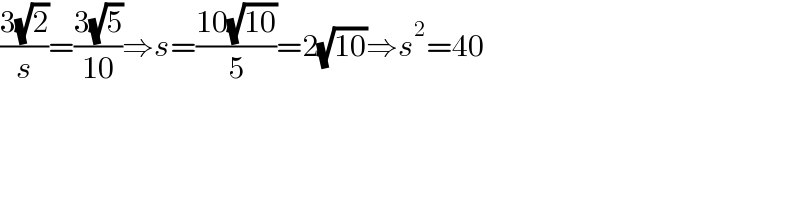
((3(√2))/s)=((3(√5))/(10))⇒s=((10(√(10)))/5)=2(√(10))⇒s^2 =40

$$\frac{\mathrm{3}\sqrt{\mathrm{2}}}{{s}}=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}\Rightarrow{s}=\frac{\mathrm{10}\sqrt{\mathrm{10}}}{\mathrm{5}}=\mathrm{2}\sqrt{\mathrm{10}}\Rightarrow{s}^{\mathrm{2}} =\mathrm{40} \\ $$

Commented by Tawa11 last updated on 17/Jun/24

Thanks sir

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 17/Jun/24

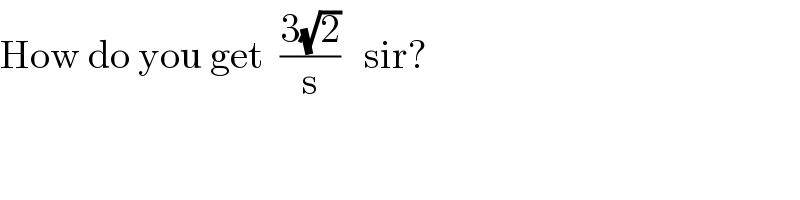
How do you get ((3(√2))/s) sir?

$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}\:\:\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{s}}\:\:\:\mathrm{sir}? \\ $$

Commented by A5T last updated on 17/Jun/24

Commented by A5T last updated on 17/Jun/24

Construct say BD=BE=3⇒DE=3(√2), and construct DF=FG=EG=3(√2) ⇒BF=3(√5);BH=r=10 Homothety that maps FG to HI gives the desired square and maps the constructed square above to another square with the desired coincident properties. This homothety has ratio ((BF)/(BH))=((3(√5))/r)=((3(√5))/(10)) which is also equal to ((FG)/(HI))=((3(√2))/s) ⇒((3(√5))/(10))=((3(√2))/s)⇒s=((10(√(10)))/5)=2(√(10))

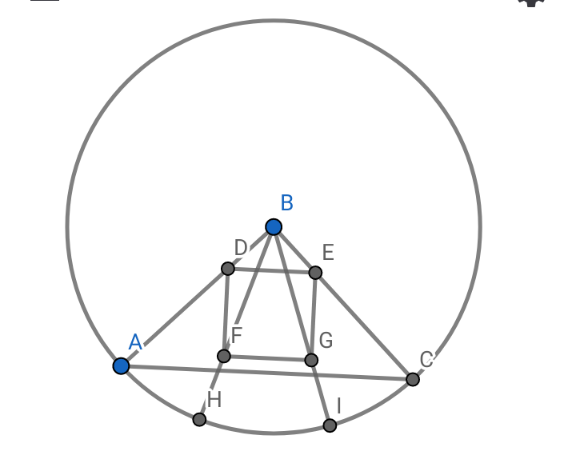
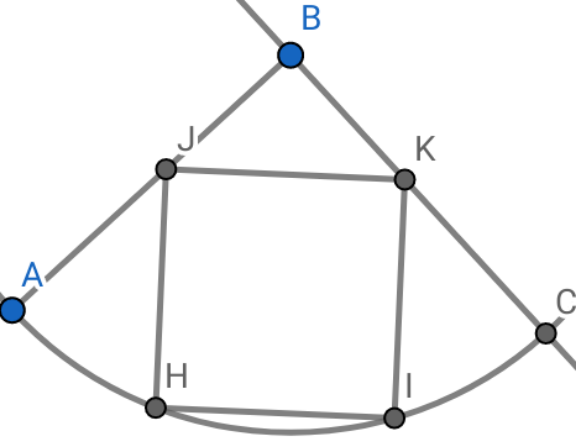
$${Construct}\:{say}\:{BD}={BE}=\mathrm{3}\Rightarrow{DE}=\mathrm{3}\sqrt{\mathrm{2}},\: \\ $$$${and}\:{construct}\:{DF}={FG}={EG}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{BF}=\mathrm{3}\sqrt{\mathrm{5}};{BH}={r}=\mathrm{10} \\ $$$${Homothety}\:{that}\:{maps}\:{FG}\:{to}\:{HI}\:{gives}\:{the} \\ $$$${desired}\:{square}\:{and}\:{maps}\:{the}\:{constructed}\:{square} \\ $$$${above}\:{to}\:{another}\:{square}\:{with}\:{the}\:{desired}\: \\ $$$${coincident}\:{properties}.\:{This}\:{homothety}\:{has}\:{ratio} \\ $$$$\frac{{BF}}{{BH}}=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{{r}}=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}\:{which}\:{is}\:{also}\:{equal}\:{to}\:\frac{{FG}}{{HI}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{{s}} \\ $$$$\Rightarrow\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{{s}}\Rightarrow{s}=\frac{\mathrm{10}\sqrt{\mathrm{10}}}{\mathrm{5}}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$

Commented by A5T last updated on 17/Jun/24

Commented by A5T last updated on 17/Jun/24

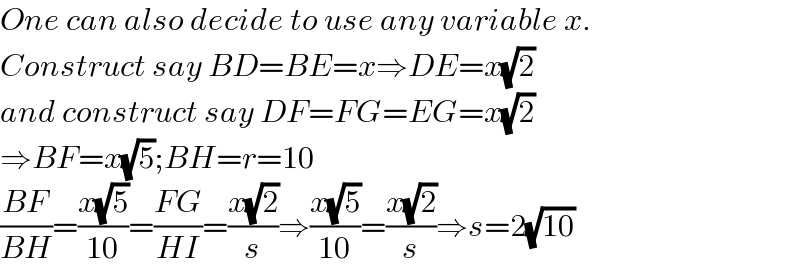
One can also decide to use any variable x. Construct say BD=BE=x⇒DE=x(√2) and construct say DF=FG=EG=x(√2) ⇒BF=x(√5);BH=r=10 ((BF)/(BH))=((x(√5))/(10))=((FG)/(HI))=((x(√2))/s)⇒((x(√5))/(10))=((x(√2))/s)⇒s=2(√(10))

$${One}\:{can}\:{also}\:{decide}\:{to}\:{use}\:{any}\:{variable}\:{x}. \\ $$$${Construct}\:{say}\:{BD}={BE}={x}\Rightarrow{DE}={x}\sqrt{\mathrm{2}} \\ $$$${and}\:{construct}\:{say}\:{DF}={FG}={EG}={x}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{BF}={x}\sqrt{\mathrm{5}};{BH}={r}=\mathrm{10} \\ $$$$\frac{{BF}}{{BH}}=\frac{{x}\sqrt{\mathrm{5}}}{\mathrm{10}}=\frac{{FG}}{{HI}}=\frac{{x}\sqrt{\mathrm{2}}}{{s}}\Rightarrow\frac{{x}\sqrt{\mathrm{5}}}{\mathrm{10}}=\frac{{x}\sqrt{\mathrm{2}}}{{s}}\Rightarrow{s}=\mathrm{2}\sqrt{\mathrm{10}} \\ $$

Commented by Tawa11 last updated on 17/Jun/24

Wow, I appreciate sir.

$$\mathrm{Wow},\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com