Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

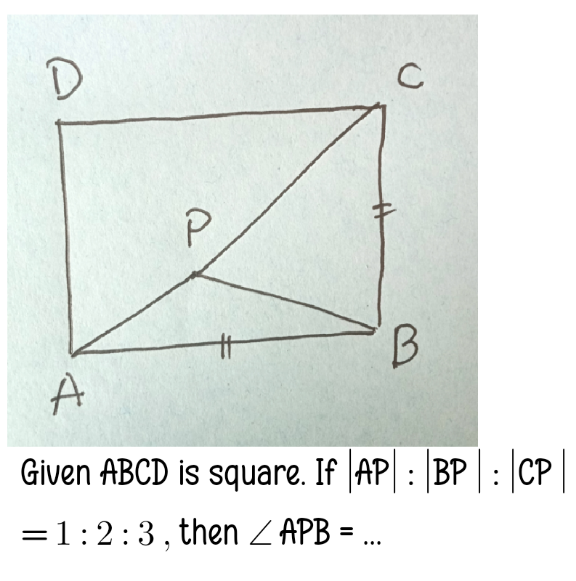
Question Number 208385 by efronzo1 last updated on 14/Jun/24

Commented by efronzo1 last updated on 15/Jun/24

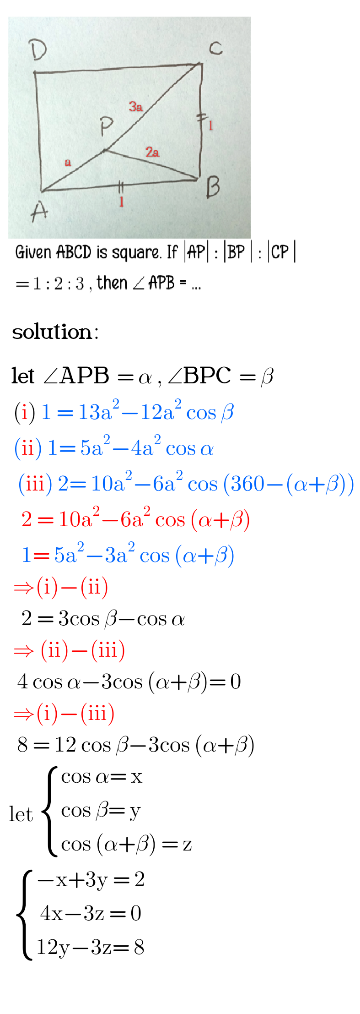
Commented by efronzo1 last updated on 15/Jun/24

i′m stuck this step

$$\mathrm{i}'\mathrm{m}\:\mathrm{stuck}\:\mathrm{this}\:\mathrm{step} \\ $$

Commented by mr W last updated on 15/Jun/24

⇒y=((2+x)/3) ⇒z=((4x)/3) cos (α+β)=cos α cos β−(√((1−cos^2 α)(1−cos^2 β))) z=xy−(√((1−x^2 )(1−y^2 ))) (xy−z)^2 =(1−x^2 )(1−y^2 ) x^2 y^2 +z^2 −2xyz=1−x^2 −y^2 +x^2 y^2 z^2 −2xyz=1−x^2 −y^2 ((16x^2 )/9)−((8x^2 (2+x))/9)=1−x^2 −(((2+x)^2 )/9) 8x^3 −10x^2 −4x+5=0 ⇒x=±((√2)/2), (5/4) only x=−((√2)/2) is suitable cos α=x=−((√2)/2) ⇒α=135°

$$\Rightarrow{y}=\frac{\mathrm{2}+{x}}{\mathrm{3}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{4}{x}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta−\sqrt{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha\right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\beta\right)} \\ $$$${z}={xy}−\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)} \\ $$$$\left({xy}−{z}\right)^{\mathrm{2}} =\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{xyz}=\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} −\mathrm{2}{xyz}=\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$$\frac{\mathrm{16}{x}^{\mathrm{2}} }{\mathrm{9}}−\frac{\mathrm{8}{x}^{\mathrm{2}} \left(\mathrm{2}+{x}\right)}{\mathrm{9}}=\mathrm{1}−{x}^{\mathrm{2}} −\frac{\left(\mathrm{2}+{x}\right)^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\mathrm{8}{x}^{\mathrm{3}} −\mathrm{10}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{x}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${only}\:{x}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{is}\:{suitable} \\ $$$$\mathrm{cos}\:\alpha={x}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\Rightarrow\alpha=\mathrm{135}° \\ $$

Answered by mr W last updated on 14/Jun/24

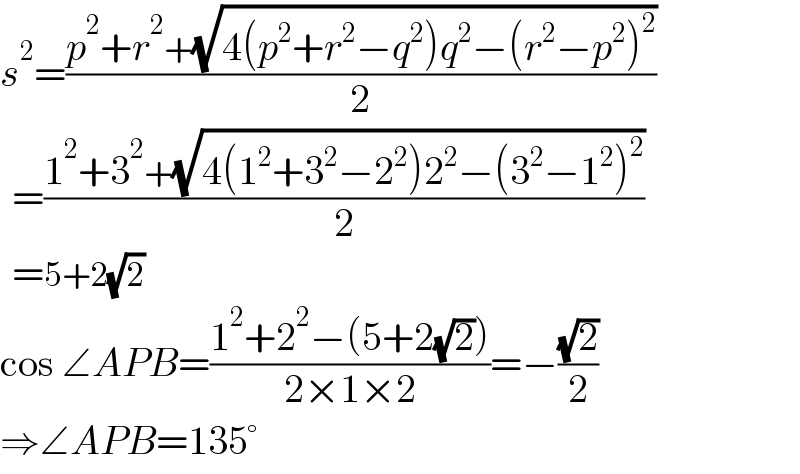
s^2 =((p^2 +r^2 +(√(4(p^2 +r^2 −q^2 )q^2 −(r^2 −p^2 )^2 )))/2) =((1^2 +3^2 +(√(4(1^2 +3^2 −2^2 )2^2 −(3^2 −1^2 )^2 )))/2) =5+2(√2) cos ∠APB=((1^2 +2^2 −(5+2(√2)))/(2×1×2))=−((√2)/2) ⇒∠APB=135°

$${s}^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} +{r}^{\mathrm{2}} +\sqrt{\mathrm{4}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −{q}^{\mathrm{2}} \right){q}^{\mathrm{2}} −\left({r}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\:\:=\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{4}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \right)\mathrm{2}^{\mathrm{2}} −\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\:\:=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mathrm{cos}\:\angle{APB}=\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}\right)}{\mathrm{2}×\mathrm{1}×\mathrm{2}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\angle{APB}=\mathrm{135}° \\ $$

Commented by efronzo1 last updated on 14/Jun/24

what

$$\mathrm{what}\:\:\: \\ $$

Commented by mr W last updated on 15/Jun/24

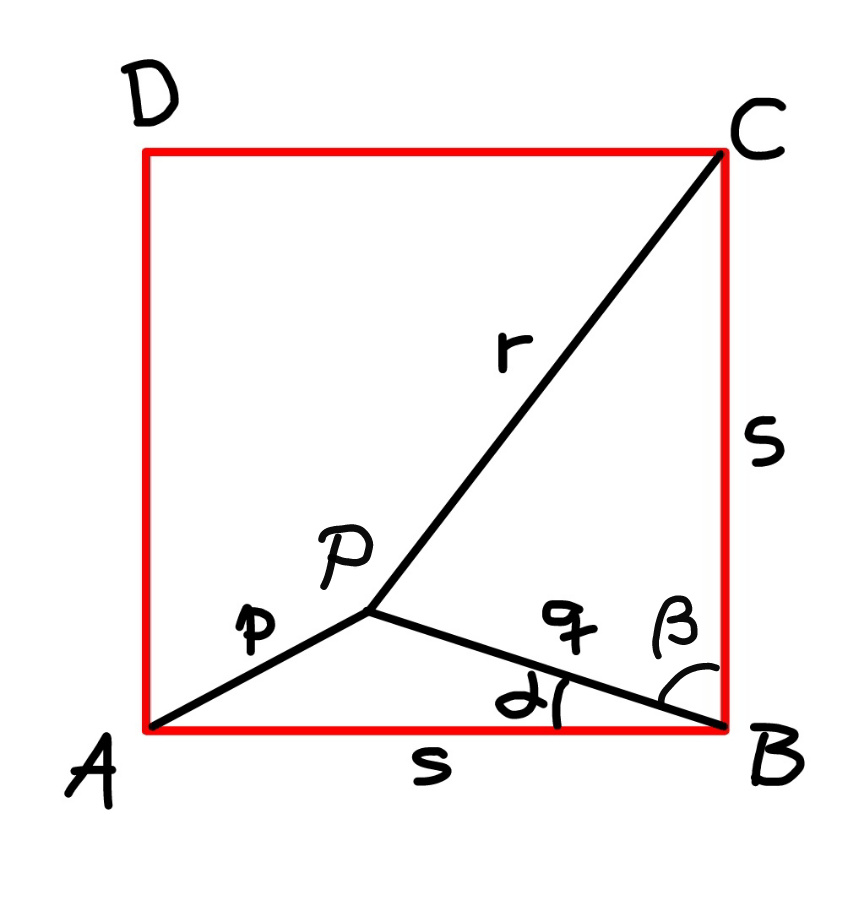
Commented by mr W last updated on 15/Jun/24

cos α=((s^2 +q^2 −p^2 )/(2qs)) sin α=cos β=((s^2 +q^2 −r^2 )/(2qs)) (((s^2 +q^2 −p^2 )/(2qs)))^2 +(((s^2 +q^2 −r^2 )/(2qs)))^2 =1 (s^2 +q^2 −p^2 )^2 +(s^2 +q^2 −r^2 )^2 =4q^2 s^2 2s^4 −2(p^2 +r^2 )s^2 +p^4 +r^4 +2q^4 −2(p^2 +r^2 )q^2 =0 ⇒s^2 =((p^2 +r^2 ±(√(4(p^2 +r^2 −q^2 )q^2 −(r^2 −p^2 )^2 )))/2) + for point P inside the square − for point P outside the square

$$\mathrm{cos}\:\alpha=\frac{{s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{2}{qs}} \\ $$$$\mathrm{sin}\:\alpha=\mathrm{cos}\:\beta=\frac{{s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}{qs}} \\ $$$$\left(\frac{{s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }{\mathrm{2}{qs}}\right)^{\mathrm{2}} +\left(\frac{{s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}{qs}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({s}^{\mathrm{2}} +{q}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{q}^{\mathrm{2}} {s}^{\mathrm{2}} \\ $$$$\mathrm{2}{s}^{\mathrm{4}} −\mathrm{2}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){s}^{\mathrm{2}} +{p}^{\mathrm{4}} +{r}^{\mathrm{4}} +\mathrm{2}{q}^{\mathrm{4}} −\mathrm{2}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){q}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} +{r}^{\mathrm{2}} \pm\sqrt{\mathrm{4}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} −{q}^{\mathrm{2}} \right){q}^{\mathrm{2}} −\left({r}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$+\:{for}\:{point}\:{P}\:{inside}\:{the}\:{square} \\ $$$$−\:{for}\:{point}\:{P}\:{outside}\:{the}\:{square} \\ $$

Commented by Tawa11 last updated on 21/Jun/24

Weldone sir.

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com