
Question Number 208288 by efronzo1 last updated on 10/Jun/24
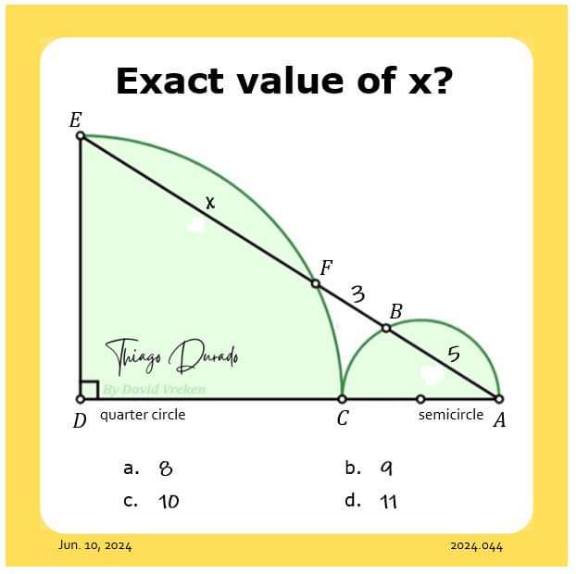
Answered by A5T last updated on 10/Jun/24
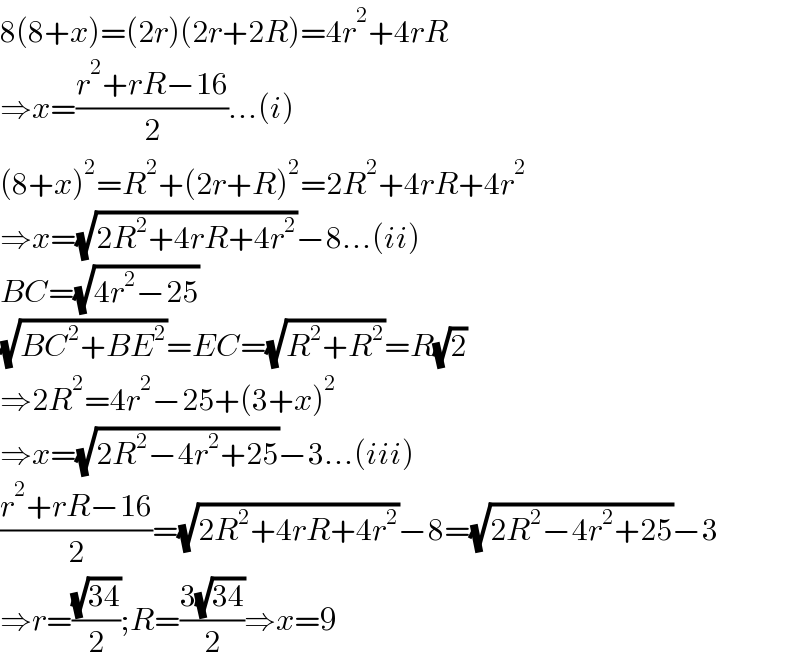
$$\mathrm{8}\left(\mathrm{8}+{x}\right)=\left(\mathrm{2}{r}\right)\left(\mathrm{2}{r}+\mathrm{2}{R}\right)=\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{rR} \\ $$$$\Rightarrow{x}=\frac{{r}^{\mathrm{2}} +{rR}−\mathrm{16}}{\mathrm{2}}...\left({i}\right) \\ $$$$\left(\mathrm{8}+{x}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +\left(\mathrm{2}{r}+{R}\right)^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} +\mathrm{4}{rR}+\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{4}{rR}+\mathrm{4}{r}^{\mathrm{2}} }−\mathrm{8}...\left({ii}\right) \\ $$$${BC}=\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\mathrm{25}} \\ $$$$\sqrt{{BC}^{\mathrm{2}} +{BE}^{\mathrm{2}} }={EC}=\sqrt{{R}^{\mathrm{2}} +{R}^{\mathrm{2}} }={R}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{R}^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} −\mathrm{25}+\left(\mathrm{3}+{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{2}{R}^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} +\mathrm{25}}−\mathrm{3}...\left({iii}\right) \\ $$$$\frac{{r}^{\mathrm{2}} +{rR}−\mathrm{16}}{\mathrm{2}}=\sqrt{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{4}{rR}+\mathrm{4}{r}^{\mathrm{2}} }−\mathrm{8}=\sqrt{\mathrm{2}{R}^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} +\mathrm{25}}−\mathrm{3} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{34}}}{\mathrm{2}};{R}=\frac{\mathrm{3}\sqrt{\mathrm{34}}}{\mathrm{2}}\Rightarrow{x}=\mathrm{9} \\ $$
Answered by mr W last updated on 10/Jun/24
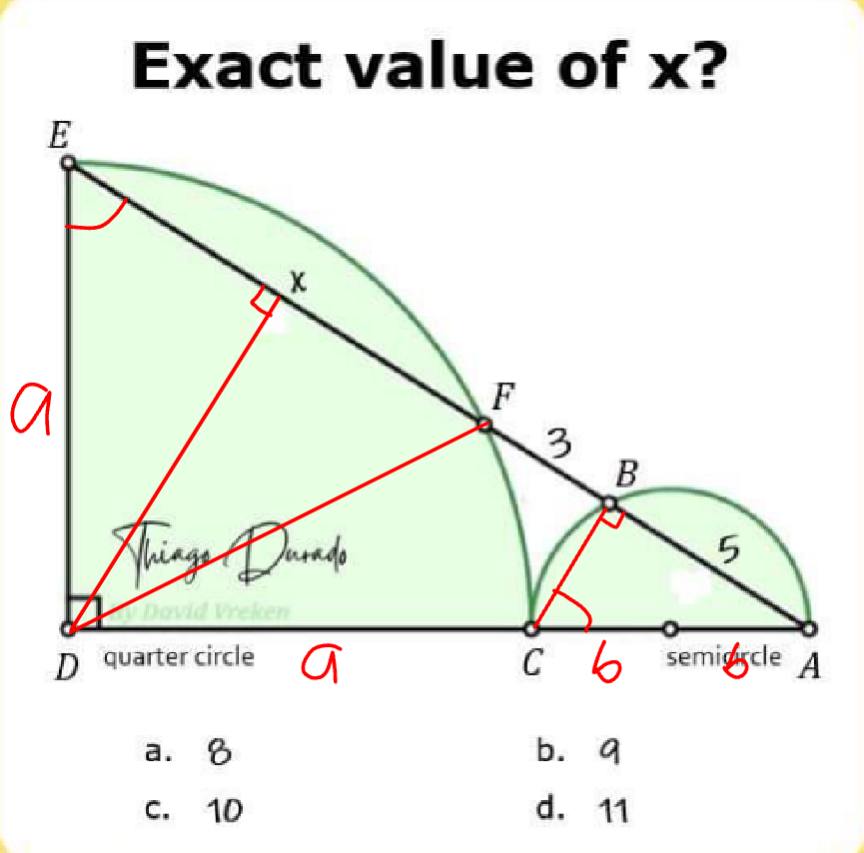
Commented by mr W last updated on 12/Jun/24
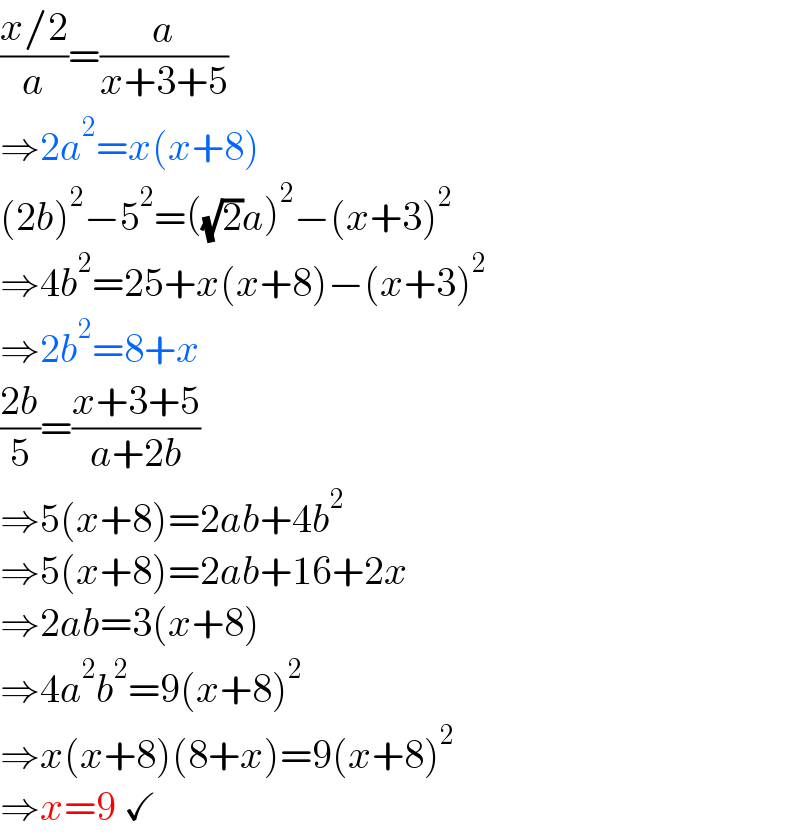
$$\frac{{x}/\mathrm{2}}{{a}}=\frac{{a}}{{x}+\mathrm{3}+\mathrm{5}}\: \\ $$$$\Rightarrow\mathrm{2}{a}^{\mathrm{2}} ={x}\left({x}+\mathrm{8}\right) \\ $$$$\left(\mathrm{2}{b}\right)^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} =\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} −\left({x}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{b}^{\mathrm{2}} =\mathrm{25}+{x}\left({x}+\mathrm{8}\right)−\left({x}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{b}^{\mathrm{2}} =\mathrm{8}+{x} \\ $$$$\frac{\mathrm{2}{b}}{\mathrm{5}}=\frac{{x}+\mathrm{3}+\mathrm{5}}{{a}+\mathrm{2}{b}} \\ $$$$\Rightarrow\mathrm{5}\left({x}+\mathrm{8}\right)=\mathrm{2}{ab}+\mathrm{4}{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{5}\left({x}+\mathrm{8}\right)=\mathrm{2}{ab}+\mathrm{16}+\mathrm{2}{x} \\ $$$$\Rightarrow\mathrm{2}{ab}=\mathrm{3}\left({x}+\mathrm{8}\right) \\ $$$$\Rightarrow\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{9}\left({x}+\mathrm{8}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}\left({x}+\mathrm{8}\right)\left(\mathrm{8}+{x}\right)=\mathrm{9}\left({x}+\mathrm{8}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{9}\:\checkmark \\ $$
Commented by Tawa11 last updated on 21/Jun/24

$$\mathrm{Nice}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{learning}\:\mathrm{questions}\:\mathrm{like}\:\mathrm{this}. \\ $$
