Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

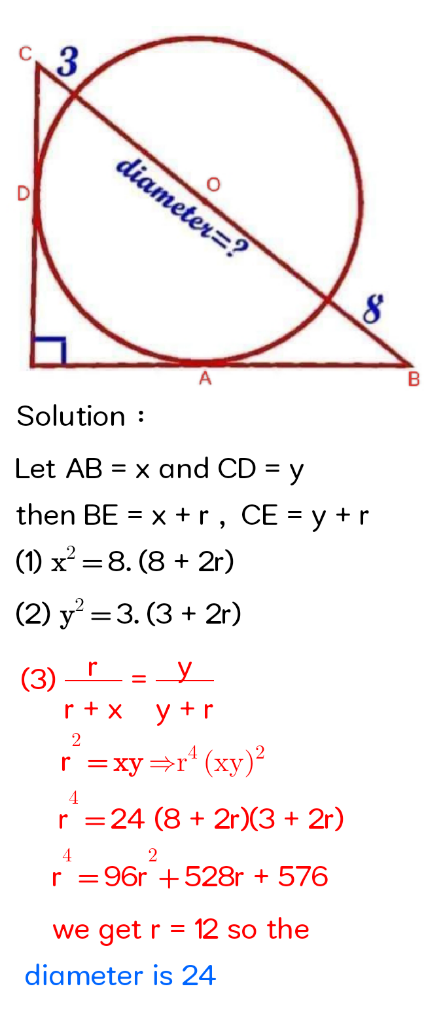
Question Number 208021 by efronzo1 last updated on 02/Jun/24

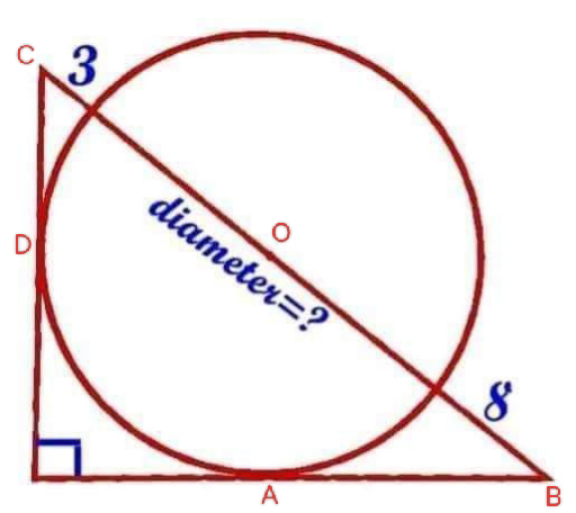
Answered by A5T last updated on 02/Jun/24

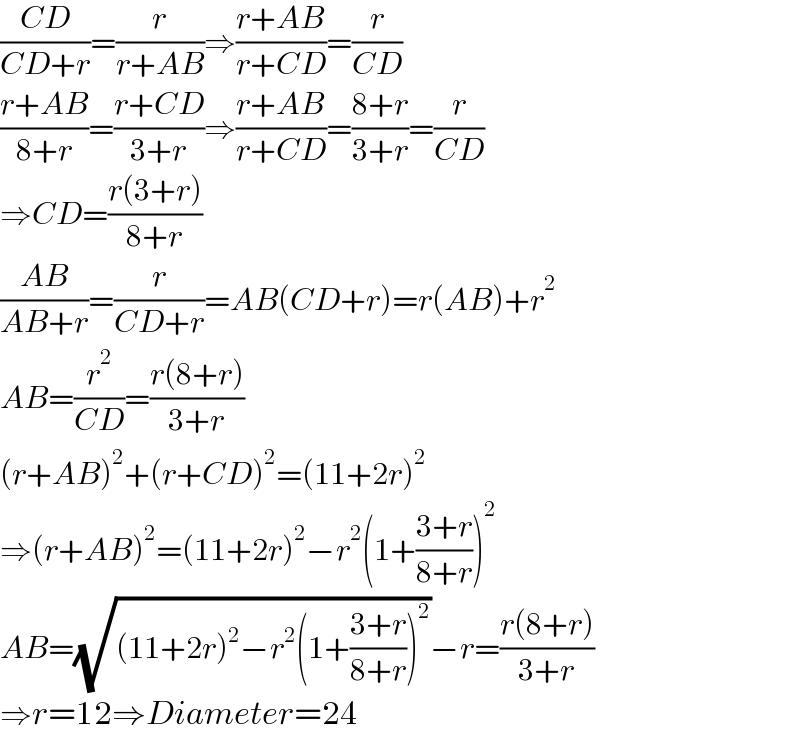
((CD)/(CD+r))=(r/(r+AB))⇒((r+AB)/(r+CD))=(r/(CD)) ((r+AB)/(8+r))=((r+CD)/(3+r))⇒((r+AB)/(r+CD))=((8+r)/(3+r))=(r/(CD)) ⇒CD=((r(3+r))/(8+r)) ((AB)/(AB+r))=(r/(CD+r))=AB(CD+r)=r(AB)+r^2 AB=(r^2 /(CD))=((r(8+r))/(3+r)) (r+AB)^2 +(r+CD)^2 =(11+2r)^2 ⇒(r+AB)^2 =(11+2r)^2 −r^2 (1+((3+r)/(8+r)))^2 AB=(√((11+2r)^2 −r^2 (1+((3+r)/(8+r)))^2 ))−r=((r(8+r))/(3+r)) ⇒r=12⇒Diameter=24

$$\frac{{CD}}{{CD}+{r}}=\frac{{r}}{{r}+{AB}}\Rightarrow\frac{{r}+{AB}}{{r}+{CD}}=\frac{{r}}{{CD}} \\ $$$$\frac{{r}+{AB}}{\mathrm{8}+{r}}=\frac{{r}+{CD}}{\mathrm{3}+{r}}\Rightarrow\frac{{r}+{AB}}{{r}+{CD}}=\frac{\mathrm{8}+{r}}{\mathrm{3}+{r}}=\frac{{r}}{{CD}} \\ $$$$\Rightarrow{CD}=\frac{{r}\left(\mathrm{3}+{r}\right)}{\mathrm{8}+{r}} \\ $$$$\frac{{AB}}{{AB}+{r}}=\frac{{r}}{{CD}+{r}}={AB}\left({CD}+{r}\right)={r}\left({AB}\right)+{r}^{\mathrm{2}} \\ $$$${AB}=\frac{{r}^{\mathrm{2}} }{{CD}}=\frac{{r}\left(\mathrm{8}+{r}\right)}{\mathrm{3}+{r}} \\ $$$$\left({r}+{AB}\right)^{\mathrm{2}} +\left({r}+{CD}\right)^{\mathrm{2}} =\left(\mathrm{11}+\mathrm{2}{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left({r}+{AB}\right)^{\mathrm{2}} =\left(\mathrm{11}+\mathrm{2}{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{3}+{r}}{\mathrm{8}+{r}}\right)^{\mathrm{2}} \\ $$$${AB}=\sqrt{\left(\mathrm{11}+\mathrm{2}{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{3}+{r}}{\mathrm{8}+{r}}\right)^{\mathrm{2}} }−{r}=\frac{{r}\left(\mathrm{8}+{r}\right)}{\mathrm{3}+{r}} \\ $$$$\Rightarrow{r}=\mathrm{12}\Rightarrow{Diameter}=\mathrm{24} \\ $$

Answered by A5T last updated on 02/Jun/24

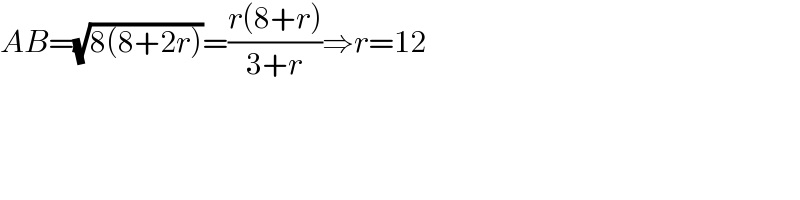
AB=(√(8(8+2r)))=((r(8+r))/(3+r))⇒r=12

$${AB}=\sqrt{\mathrm{8}\left(\mathrm{8}+\mathrm{2}{r}\right)}=\frac{{r}\left(\mathrm{8}+{r}\right)}{\mathrm{3}+{r}}\Rightarrow{r}=\mathrm{12} \\ $$

Answered by A5T last updated on 02/Jun/24

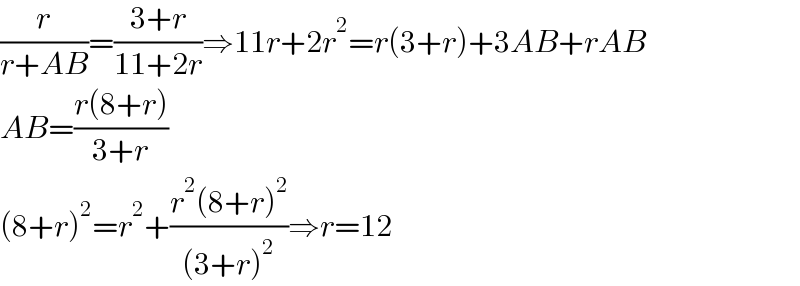
(r/(r+AB))=((3+r)/(11+2r))⇒11r+2r^2 =r(3+r)+3AB+rAB AB=((r(8+r))/(3+r)) (8+r)^2 =r^2 +((r^2 (8+r)^2 )/((3+r)^2 ))⇒r=12

$$\frac{{r}}{{r}+{AB}}=\frac{\mathrm{3}+{r}}{\mathrm{11}+\mathrm{2}{r}}\Rightarrow\mathrm{11}{r}+\mathrm{2}{r}^{\mathrm{2}} ={r}\left(\mathrm{3}+{r}\right)+\mathrm{3}{AB}+{rAB} \\ $$$${AB}=\frac{{r}\left(\mathrm{8}+{r}\right)}{\mathrm{3}+{r}} \\ $$$$\left(\mathrm{8}+{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} \left(\mathrm{8}+{r}\right)^{\mathrm{2}} }{\left(\mathrm{3}+{r}\right)^{\mathrm{2}} }\Rightarrow{r}=\mathrm{12} \\ $$

Answered by efronzo1 last updated on 02/Jun/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com