
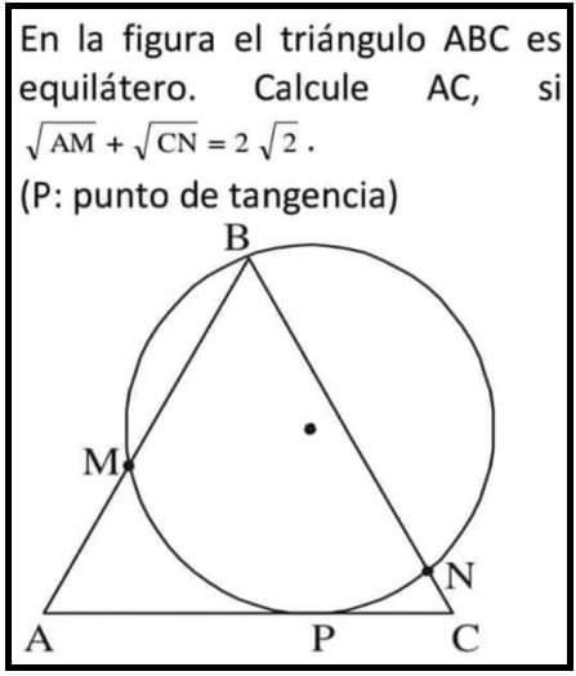
Question Number 207985 by efronzo1 last updated on 02/Jun/24
Answered by mr W last updated on 02/Jun/24
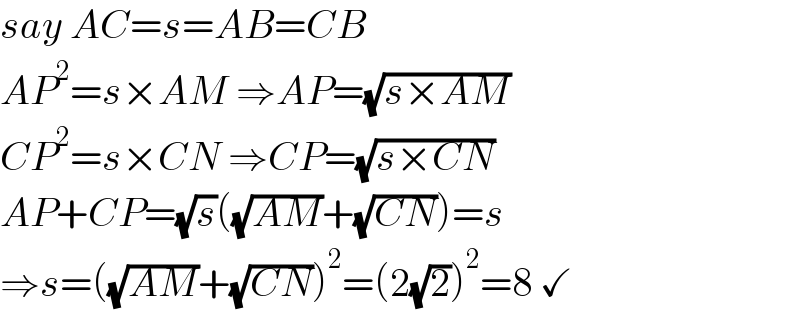
$${say}\:{AC}={s}={AB}={CB} \\ $$$${AP}^{\mathrm{2}} ={s}×{AM}\:\Rightarrow{AP}=\sqrt{{s}×{AM}} \\ $$$${CP}^{\mathrm{2}} ={s}×{CN}\:\Rightarrow{CP}=\sqrt{{s}×{CN}} \\ $$$${AP}+{CP}=\sqrt{{s}}\left(\sqrt{{AM}}+\sqrt{{CN}}\right)={s} \\ $$$$\Rightarrow{s}=\left(\sqrt{{AM}}+\sqrt{{CN}}\right)^{\mathrm{2}} =\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{8}\:\checkmark \\ $$
Commented by Tawa11 last updated on 21/Jun/24
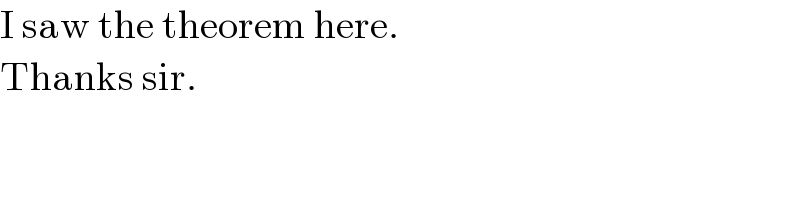
$$\mathrm{I}\:\mathrm{saw}\:\mathrm{the}\:\mathrm{theorem}\:\mathrm{here}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
