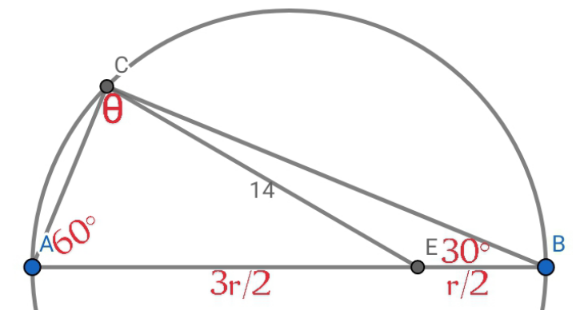
Question Number 207731 by efronzo1 last updated on 24/May/24

$$\:\:\:\downharpoonleft\underline{\:} \\ $$
Answered by A5T last updated on 24/May/24
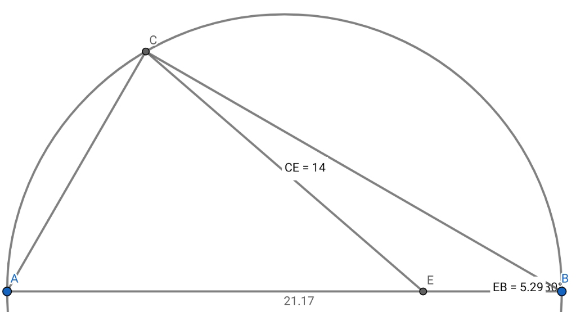
Commented by A5T last updated on 24/May/24
![∠ACE=θ⇒∠BCE=90−θ⇒∠CEB=60+θ ((sinθ)/((3r)/2))=((sin60)/(14))⇒sinθ=((3(√3)r)/(56))...(i) ((sin(90−θ))/(r/2))=((sin30)/(14))⇒cosθ=(r/(56))...(ii) (((i))/((ii)))⇒tanθ=3(√3)⇒θ=tan^(−1) (3(√3)) [BCE]=(1/2)×(r/2)×14×sin(60+θ) =7×28cos(tan^(−1) (3(√3)))sin(60+tan^(−1) (3(√3))) ≈24.249](Q207734.png)
$$\angle{ACE}=\theta\Rightarrow\angle{BCE}=\mathrm{90}−\theta\Rightarrow\angle{CEB}=\mathrm{60}+\theta \\ $$$$\frac{{sin}\theta}{\frac{\mathrm{3}{r}}{\mathrm{2}}}=\frac{{sin}\mathrm{60}}{\mathrm{14}}\Rightarrow{sin}\theta=\frac{\mathrm{3}\sqrt{\mathrm{3}}{r}}{\mathrm{56}}...\left({i}\right) \\ $$$$\frac{{sin}\left(\mathrm{90}−\theta\right)}{\frac{{r}}{\mathrm{2}}}=\frac{{sin}\mathrm{30}}{\mathrm{14}}\Rightarrow{cos}\theta=\frac{{r}}{\mathrm{56}}...\left({ii}\right) \\ $$$$\frac{\left({i}\right)}{\left({ii}\right)}\Rightarrow{tan}\theta=\mathrm{3}\sqrt{\mathrm{3}}\Rightarrow\theta={tan}^{−\mathrm{1}} \left(\mathrm{3}\sqrt{\mathrm{3}}\right) \\ $$$$\left[{BCE}\right]=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{r}}{\mathrm{2}}×\mathrm{14}×{sin}\left(\mathrm{60}+\theta\right) \\ $$$$=\mathrm{7}×\mathrm{28}{cos}\left({tan}^{−\mathrm{1}} \left(\mathrm{3}\sqrt{\mathrm{3}}\right)\right){sin}\left(\mathrm{60}+{tan}^{−\mathrm{1}} \left(\mathrm{3}\sqrt{\mathrm{3}}\right)\right) \\ $$$$\approx\mathrm{24}.\mathrm{249} \\ $$
Answered by A5T last updated on 24/May/24
![sinθ=((3(√3)r)/(56));cosθ=(r/(56))⇒sinθ=3(√3)cosθ ⇒sinθ=3(√(3(1−sin^2 θ)))⇒sin^2 θ=27(1−sin^2 θ) ⇒28sin^2 θ=27⇒sinθ=((3(√(21)))/(14)) ⇒r=((56sinθ)/(3(√3)))=((12(√(21)))/(3(√3)))=4(√7) sin(60+θ)=sin60cosθ+cos60sinθ =((√3)/2)×((√7)/(14))+(1/2)×((3(√(21)))/(14))=((√(21))/7) ⇒[BCE]=(1/2)×14×2(√7)×((√(21))/7)=14(√3)](Q207735.png)
$${sin}\theta=\frac{\mathrm{3}\sqrt{\mathrm{3}}{r}}{\mathrm{56}};{cos}\theta=\frac{{r}}{\mathrm{56}}\Rightarrow{sin}\theta=\mathrm{3}\sqrt{\mathrm{3}}{cos}\theta \\ $$$$\Rightarrow{sin}\theta=\mathrm{3}\sqrt{\mathrm{3}\left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right)}\Rightarrow{sin}^{\mathrm{2}} \theta=\mathrm{27}\left(\mathrm{1}−{sin}^{\mathrm{2}} \theta\right) \\ $$$$\Rightarrow\mathrm{28}{sin}^{\mathrm{2}} \theta=\mathrm{27}\Rightarrow{sin}\theta=\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{56}{sin}\theta}{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\mathrm{12}\sqrt{\mathrm{21}}}{\mathrm{3}\sqrt{\mathrm{3}}}=\mathrm{4}\sqrt{\mathrm{7}} \\ $$$${sin}\left(\mathrm{60}+\theta\right)={sin}\mathrm{60}{cos}\theta+{cos}\mathrm{60}{sin}\theta \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{7}} \\ $$$$\Rightarrow\left[{BCE}\right]=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{14}×\mathrm{2}\sqrt{\mathrm{7}}×\frac{\sqrt{\mathrm{21}}}{\mathrm{7}}=\mathrm{14}\sqrt{\mathrm{3}} \\ $$
Commented by A5T last updated on 24/May/24