Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 207713 by efronzo1 last updated on 24/May/24

Answered by Berbere last updated on 24/May/24

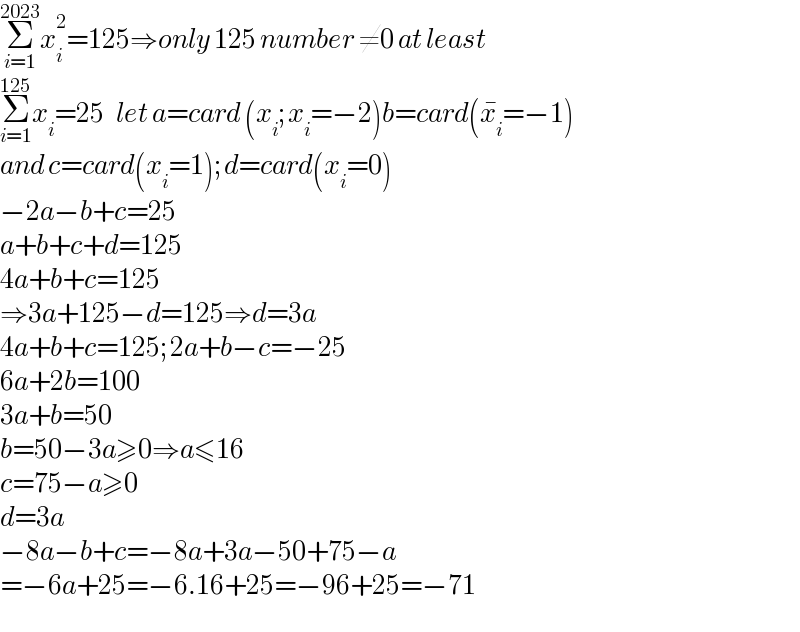
Σ_(i=1) ^(2023) x_i ^2 =125⇒only 125 number ≠0 at least Σ_(i=1) ^(125) x_i =25 let a=card (x_i ;x_i =−2)b=card(x_i ^� =−1) and c=card(x_i =1);d=card(x_i =0) −2a−b+c=25 a+b+c+d=125 4a+b+c=125 ⇒3a+125−d=125⇒d=3a 4a+b+c=125;2a+b−c=−25 6a+2b=100 3a+b=50 b=50−3a≥0⇒a≤16 c=75−a≥0 d=3a −8a−b+c=−8a+3a−50+75−a =−6a+25=−6.16+25=−96+25=−71

$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{2023}} {\sum}}{x}_{{i}} ^{\mathrm{2}} =\mathrm{125}\Rightarrow{only}\:\mathrm{125}\:{number}\:\neq\mathrm{0}\:{at}\:{least} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{125}} {\sum}}{x}_{{i}} =\mathrm{25}\:\:\:{let}\:{a}={card}\:\left({x}_{{i}} ;{x}_{{i}} =−\mathrm{2}\right){b}={card}\left(\bar {{x}}_{{i}} =−\mathrm{1}\right) \\ $$$${and}\:{c}={card}\left({x}_{{i}} =\mathrm{1}\right);{d}={card}\left({x}_{{i}} =\mathrm{0}\right) \\ $$$$−\mathrm{2}{a}−{b}+{c}=\mathrm{25} \\ $$$${a}+{b}+{c}+{d}=\mathrm{125} \\ $$$$\mathrm{4}{a}+{b}+{c}=\mathrm{125} \\ $$$$\Rightarrow\mathrm{3}{a}+\mathrm{125}−{d}=\mathrm{125}\Rightarrow{d}=\mathrm{3}{a} \\ $$$$\mathrm{4}{a}+{b}+{c}=\mathrm{125};\mathrm{2}{a}+{b}−{c}=−\mathrm{25} \\ $$$$\mathrm{6}{a}+\mathrm{2}{b}=\mathrm{100} \\ $$$$\mathrm{3}{a}+{b}=\mathrm{50} \\ $$$${b}=\mathrm{50}−\mathrm{3}{a}\geqslant\mathrm{0}\Rightarrow{a}\leqslant\mathrm{16} \\ $$$${c}=\mathrm{75}−{a}\geqslant\mathrm{0} \\ $$$${d}=\mathrm{3}{a} \\ $$$$−\mathrm{8}{a}−{b}+{c}=−\mathrm{8}{a}+\mathrm{3}{a}−\mathrm{50}+\mathrm{75}−{a} \\ $$$$=−\mathrm{6}{a}+\mathrm{25}=−\mathrm{6}.\mathrm{16}+\mathrm{25}=−\mathrm{96}+\mathrm{25}=−\mathrm{71} \\ $$

Answered by mr W last updated on 24/May/24

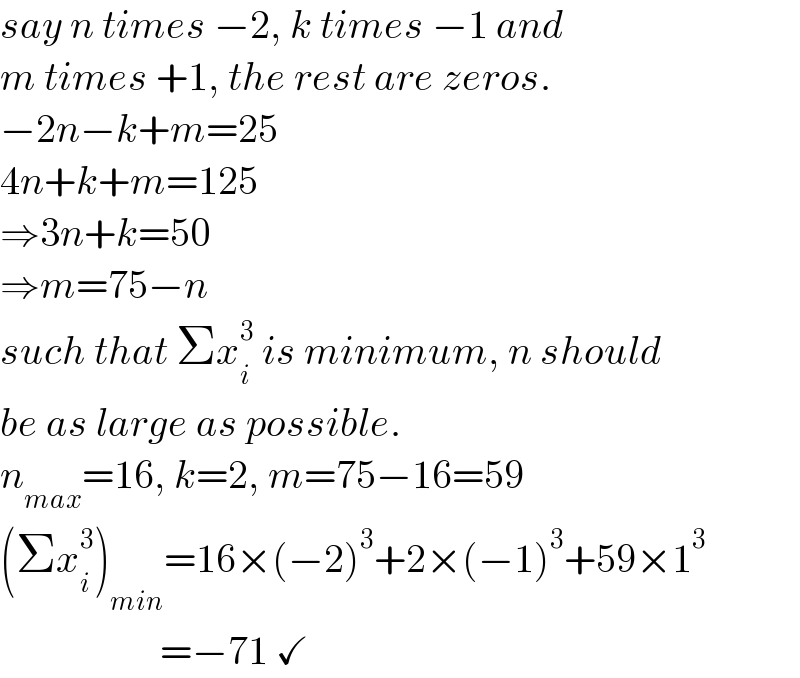
say n times −2, k times −1 and m times +1, the rest are zeros. −2n−k+m=25 4n+k+m=125 ⇒3n+k=50 ⇒m=75−n such that Σx_i ^3 is minimum, n should be as large as possible. n_(max) =16, k=2, m=75−16=59 (Σx_i ^3 )_(min) =16×(−2)^3 +2×(−1)^3 +59×1^3 =−71 ✓

$${say}\:{n}\:{times}\:−\mathrm{2},\:{k}\:{times}\:−\mathrm{1}\:{and} \\ $$$${m}\:{times}\:+\mathrm{1},\:{the}\:{rest}\:{are}\:{zeros}. \\ $$$$−\mathrm{2}{n}−{k}+{m}=\mathrm{25} \\ $$$$\mathrm{4}{n}+{k}+{m}=\mathrm{125} \\ $$$$\Rightarrow\mathrm{3}{n}+{k}=\mathrm{50} \\ $$$$\Rightarrow{m}=\mathrm{75}−{n} \\ $$$${such}\:{that}\:\Sigma{x}_{{i}} ^{\mathrm{3}} \:{is}\:{minimum},\:{n}\:{should} \\ $$$${be}\:{as}\:{large}\:{as}\:{possible}. \\ $$$${n}_{{max}} =\mathrm{16},\:{k}=\mathrm{2},\:{m}=\mathrm{75}−\mathrm{16}=\mathrm{59} \\ $$$$\left(\Sigma{x}_{{i}} ^{\mathrm{3}} \right)_{{min}} =\mathrm{16}×\left(−\mathrm{2}\right)^{\mathrm{3}} +\mathrm{2}×\left(−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{59}×\mathrm{1}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{71}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com