Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 207543 by efronzo1 last updated on 18/May/24

Commented by efronzo1 last updated on 18/May/24

$$\:\: \\ $$

Answered by A5T last updated on 18/May/24

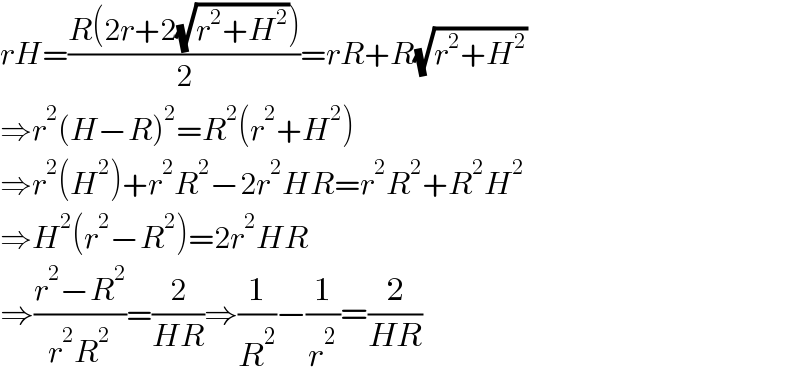
rH=((R(2r+2(√(r^2 +H^2 ))))/2)=rR+R(√(r^2 +H^2 )) ⇒r^2 (H−R)^2 =R^2 (r^2 +H^2 ) ⇒r^2 (H^2 )+r^2 R^2 −2r^2 HR=r^2 R^2 +R^2 H^2 ⇒H^2 (r^2 −R^2 )=2r^2 HR ⇒((r^2 −R^2 )/(r^2 R^2 ))=(2/(HR))⇒(1/R^2 )−(1/r^2 )=(2/(HR))

$${rH}=\frac{{R}\left(\mathrm{2}{r}+\mathrm{2}\sqrt{{r}^{\mathrm{2}} +{H}^{\mathrm{2}} }\right)}{\mathrm{2}}={rR}+{R}\sqrt{{r}^{\mathrm{2}} +{H}^{\mathrm{2}} } \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left({H}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \left({r}^{\mathrm{2}} +{H}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left({H}^{\mathrm{2}} \right)+{r}^{\mathrm{2}} {R}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} {HR}={r}^{\mathrm{2}} {R}^{\mathrm{2}} +{R}^{\mathrm{2}} {H}^{\mathrm{2}} \\ $$$$\Rightarrow{H}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{R}^{\mathrm{2}} \right)=\mathrm{2}{r}^{\mathrm{2}} {HR} \\ $$$$\Rightarrow\frac{{r}^{\mathrm{2}} −{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} {R}^{\mathrm{2}} }=\frac{\mathrm{2}}{{HR}}\Rightarrow\frac{\mathrm{1}}{{R}^{\mathrm{2}} }−\frac{\mathrm{1}}{{r}^{\mathrm{2}} }=\frac{\mathrm{2}}{{HR}} \\ $$

Answered by mr W last updated on 18/May/24

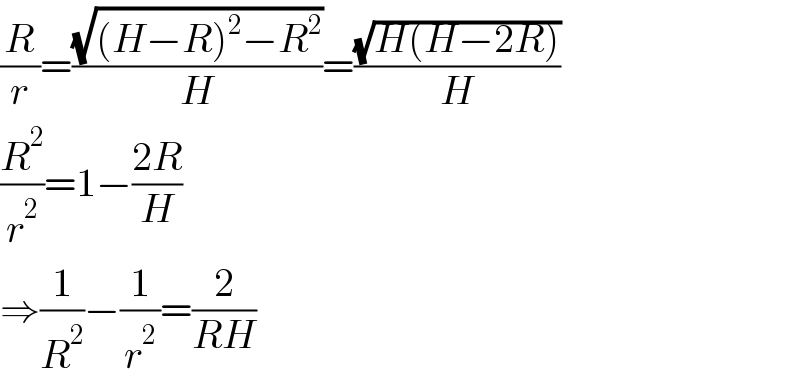
(R/r)=((√((H−R)^2 −R^2 ))/H)=((√(H(H−2R)))/H) (R^2 /r^2 )=1−((2R)/H) ⇒(1/R^2 )−(1/r^2 )=(2/(RH))

$$\frac{{R}}{{r}}=\frac{\sqrt{\left({H}−{R}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }}{{H}}=\frac{\sqrt{{H}\left({H}−\mathrm{2}{R}\right)}}{{H}} \\ $$$$\frac{{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{2}{R}}{{H}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{R}^{\mathrm{2}} }−\frac{\mathrm{1}}{{r}^{\mathrm{2}} }=\frac{\mathrm{2}}{{RH}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com