
Question Number 207426 by mr W last updated on 14/May/24
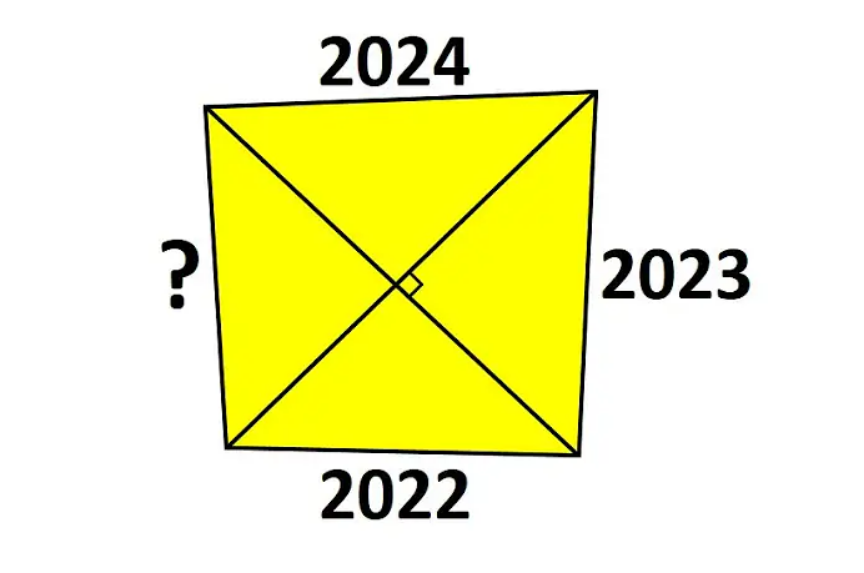
Answered by A5T last updated on 14/May/24
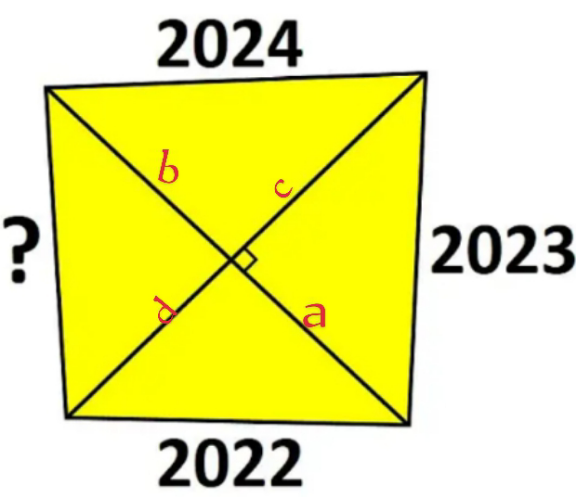
Commented by A5T last updated on 14/May/24
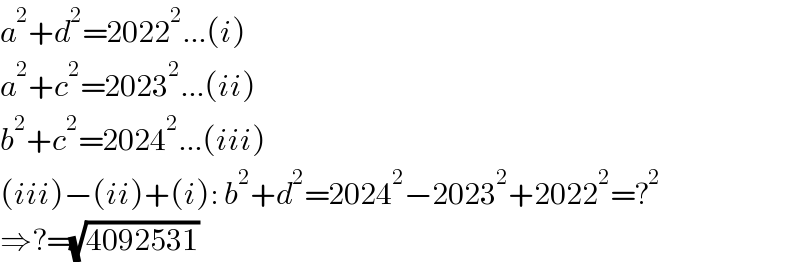
$${a}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{2022}^{\mathrm{2}} ...\left({i}\right) \\ $$$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2023}^{\mathrm{2}} ...\left({ii}\right) \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2024}^{\mathrm{2}} ...\left({iii}\right) \\ $$$$\left({iii}\right)−\left({ii}\right)+\left({i}\right):\:{b}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{2024}^{\mathrm{2}} −\mathrm{2023}^{\mathrm{2}} +\mathrm{2022}^{\mathrm{2}} =?^{\mathrm{2}} \\ $$$$\Rightarrow?=\sqrt{\mathrm{4092531}} \\ $$
Commented by mr W last updated on 14/May/24
��
