
Question Number 207423 by efronzo1 last updated on 14/May/24

$$\:\:\:\:\downharpoonleft\underline{\:} \\ $$
Answered by mr W last updated on 14/May/24
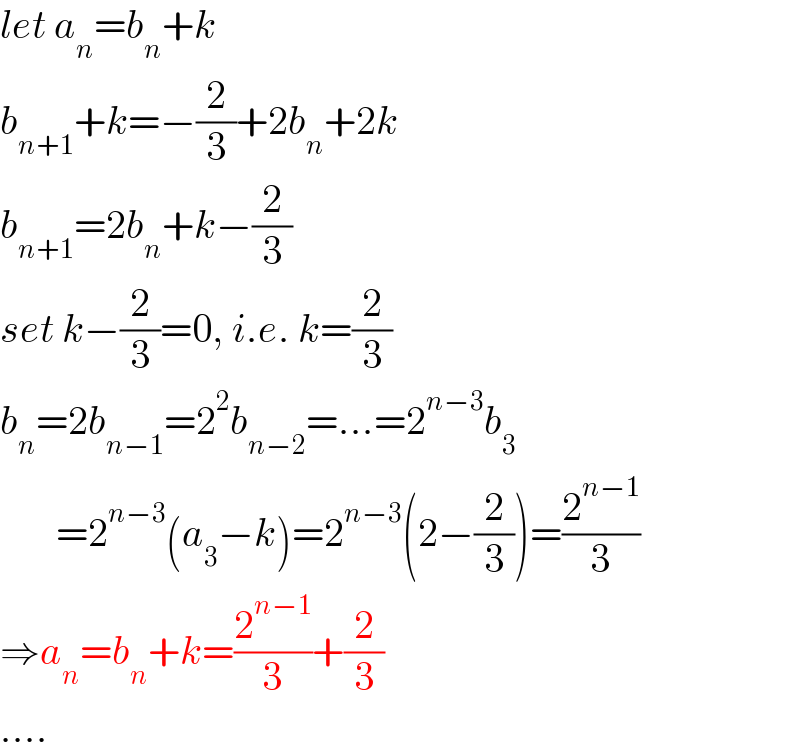
$${let}\:{a}_{{n}} ={b}_{{n}} +{k} \\ $$$${b}_{{n}+\mathrm{1}} +{k}=−\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}{b}_{{n}} +\mathrm{2}{k} \\ $$$${b}_{{n}+\mathrm{1}} =\mathrm{2}{b}_{{n}} +{k}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${set}\:{k}−\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{0},\:{i}.{e}.\:{k}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${b}_{{n}} =\mathrm{2}{b}_{{n}−\mathrm{1}} =\mathrm{2}^{\mathrm{2}} {b}_{{n}−\mathrm{2}} =...=\mathrm{2}^{{n}−\mathrm{3}} {b}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2}^{{n}−\mathrm{3}} \left({a}_{\mathrm{3}} −{k}\right)=\mathrm{2}^{{n}−\mathrm{3}} \left(\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\mathrm{3}} \\ $$$$\Rightarrow{a}_{{n}} ={b}_{{n}} +{k}=\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$.... \\ $$
Answered by AliJumaa last updated on 15/May/24

$${i}\:{have}\:{been}\:{derrived}\:{this}\:{form}\::\: \\ $$$$\begin{cases}{{u}_{{n}+\mathrm{1}} ={au}_{{n}} +{b}}\\{{u}_{{m}} ={k}}\end{cases} \\ $$$$\Rightarrow\:{u}_{{n}} ={a}^{{n}} \left(\frac{{k}+\frac{{b}}{{a}−\mathrm{1}}}{{a}^{{m}} }\right)−\frac{{b}}{{a}−\mathrm{1}} \\ $$$${a}_{{n}} =\mathrm{2}^{{n}} \left(\frac{\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{8}}\right)+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{2}^{{n}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{1}:{a}_{\mathrm{5}} =\mathrm{2}^{\mathrm{5}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{6}\:\:\:\:\:\:\mathcal{FALS} \\ $$$$\mathrm{2}:\:{a}_{{n}} \:\gneqq\mathrm{0}\:\forall{n}\in\mathbb{N}\:\:\:\:\:\:\:\mathcal{TRUE} \\ $$$${i}\:{will}\:{complete}\:{next}\:{time} \\ $$
