
Question Number 207060 by efronzo1 last updated on 06/May/24

$$\:\:\downharpoonleft\underline{\:} \\ $$
Answered by mr W last updated on 05/May/24
![Method II a_(n+2) −a_(n+1) =−(1/2)(a_(n+1) −a_n ) let b_n =a_(n+1) −a_n b_(n+1) =−(1/2)b_n b_n =(−(1/2))b_(n−1) =(−(1/2))^2 b_(n−2) =...=(−(1/2))^(n−4) b_4 a_(n+1) −a_n =(−(1/2))^(n−4) (a_5 −a_4 )=(−(1/2))^(n−4) a_(n+1) −a_n =(−(1/2))^(n−4) =16(−(1/2))^n a_n −a_(n−1) =16(−(1/2))^(n−1) a_(n−1) −a_(n−2) =16(−(1/2))^(n−2) ... a_5 −a_4 =16(−(1/2))^4 a_n −a_4 =16(−(1/2))^4 [1+(−(1/2))+(−(1/2))^2 +...+(−(1/2))^(n−5) ] a_n −a_4 =((1−(−(1/2))^(n−4) )/(1+(1/2))) a_n =(2/3)[1−(−(1/2))^(n−4) ]+4=((14)/3)−((32)/3)(−(1/2))^n](Q207071.png)
$$\underline{{Method}\:{II}} \\ $$$${a}_{{n}+\mathrm{2}} −{a}_{{n}+\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\left({a}_{{n}+\mathrm{1}} −{a}_{{n}} \right) \\ $$$${let}\:{b}_{{n}} ={a}_{{n}+\mathrm{1}} −{a}_{{n}} \\ $$$${b}_{{n}+\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}{b}_{{n}} \\ $$$${b}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right){b}_{{n}−\mathrm{1}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} {b}_{{n}−\mathrm{2}} =...=\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} {b}_{\mathrm{4}} \\ $$$${a}_{{n}+\mathrm{1}} −{a}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} \left({a}_{\mathrm{5}} −{a}_{\mathrm{4}} \right)=\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} \\ $$$${a}_{{n}+\mathrm{1}} −{a}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} =\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$${a}_{{n}} −{a}_{{n}−\mathrm{1}} =\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \\ $$$${a}_{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{2}} =\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{2}} \\ $$$$... \\ $$$${a}_{\mathrm{5}} −{a}_{\mathrm{4}} =\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} \\ $$$${a}_{{n}} −{a}_{\mathrm{4}} =\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} \left[\mathrm{1}+\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +...+\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{5}} \right] \\ $$$${a}_{{n}} −{a}_{\mathrm{4}} =\frac{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}−\mathrm{4}} \right]+\mathrm{4}=\frac{\mathrm{14}}{\mathrm{3}}−\frac{\mathrm{32}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$
Answered by mr W last updated on 05/May/24
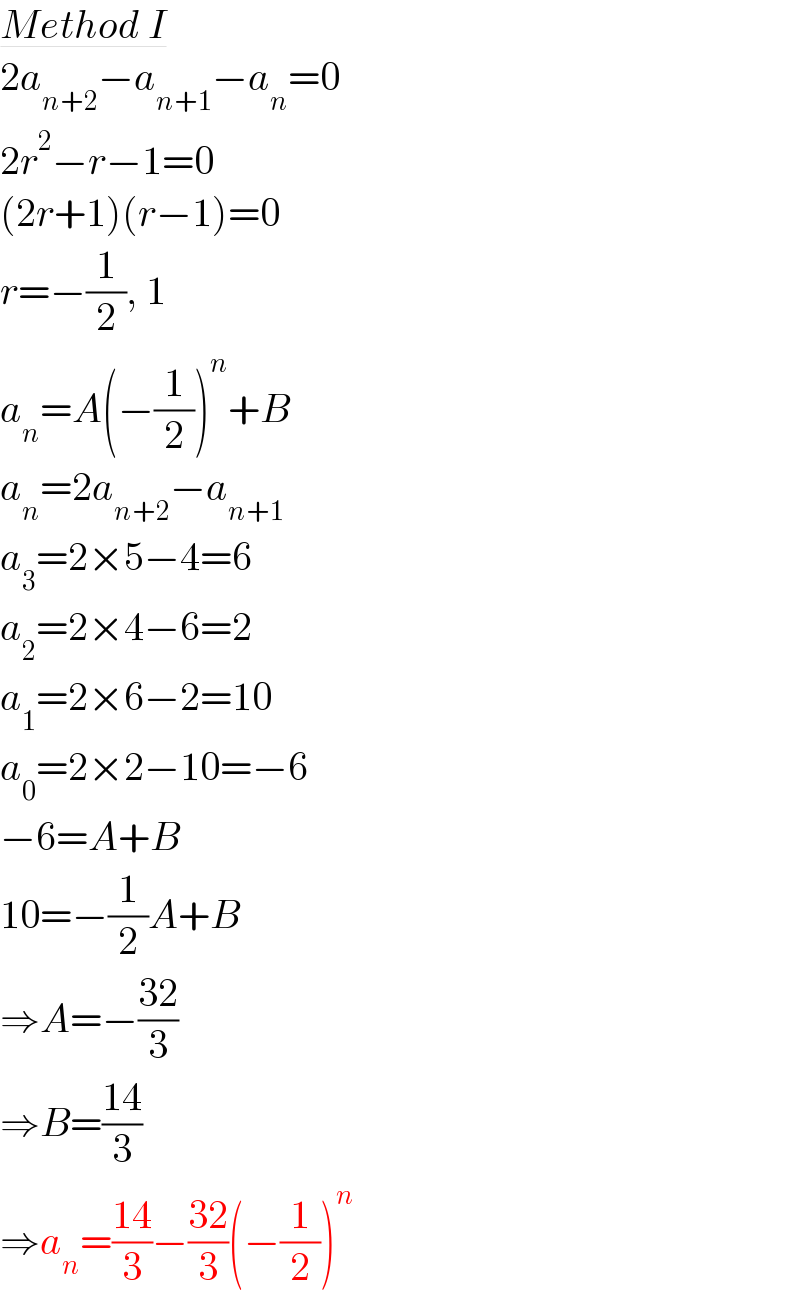
$$\underline{{Method}\:{I}} \\ $$$$\mathrm{2}{a}_{{n}+\mathrm{2}} −{a}_{{n}+\mathrm{1}} −{a}_{{n}} =\mathrm{0} \\ $$$$\mathrm{2}{r}^{\mathrm{2}} −{r}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{r}+\mathrm{1}\right)\left({r}−\mathrm{1}\right)=\mathrm{0} \\ $$$${r}=−\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{1} \\ $$$${a}_{{n}} ={A}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +{B} \\ $$$${a}_{{n}} =\mathrm{2}{a}_{{n}+\mathrm{2}} −{a}_{{n}+\mathrm{1}} \\ $$$${a}_{\mathrm{3}} =\mathrm{2}×\mathrm{5}−\mathrm{4}=\mathrm{6} \\ $$$${a}_{\mathrm{2}} =\mathrm{2}×\mathrm{4}−\mathrm{6}=\mathrm{2} \\ $$$${a}_{\mathrm{1}} =\mathrm{2}×\mathrm{6}−\mathrm{2}=\mathrm{10} \\ $$$${a}_{\mathrm{0}} =\mathrm{2}×\mathrm{2}−\mathrm{10}=−\mathrm{6} \\ $$$$−\mathrm{6}={A}+{B} \\ $$$$\mathrm{10}=−\frac{\mathrm{1}}{\mathrm{2}}{A}+{B} \\ $$$$\Rightarrow{A}=−\frac{\mathrm{32}}{\mathrm{3}} \\ $$$$\Rightarrow{B}=\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{14}}{\mathrm{3}}−\frac{\mathrm{32}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$
Commented by efronzo1 last updated on 06/May/24

