
Question Number 207018 by cherokeesay last updated on 03/May/24
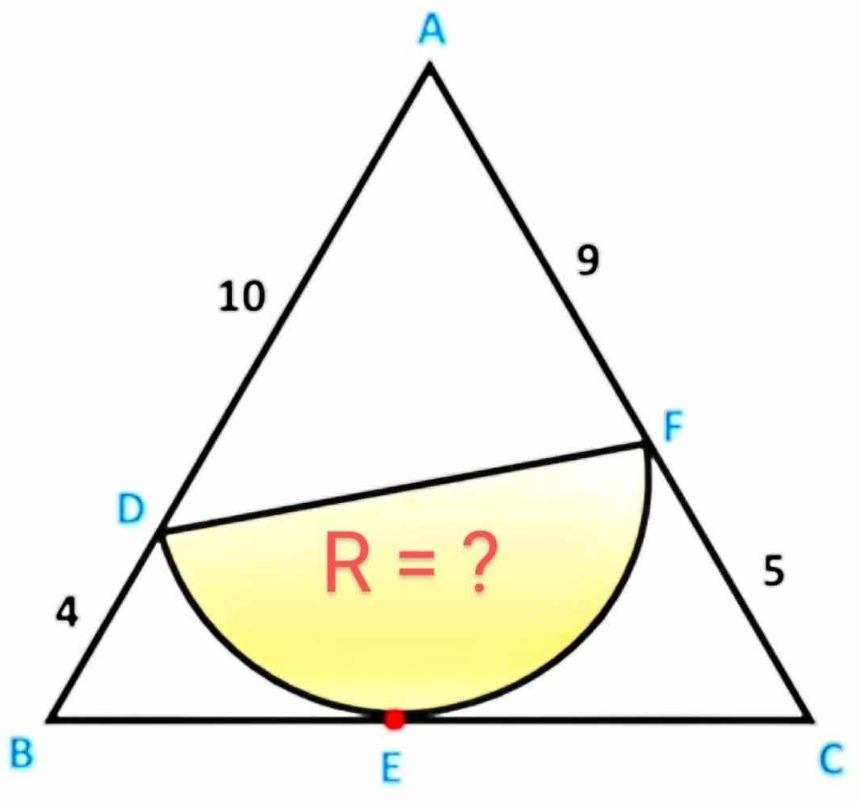
Answered by mr W last updated on 04/May/24
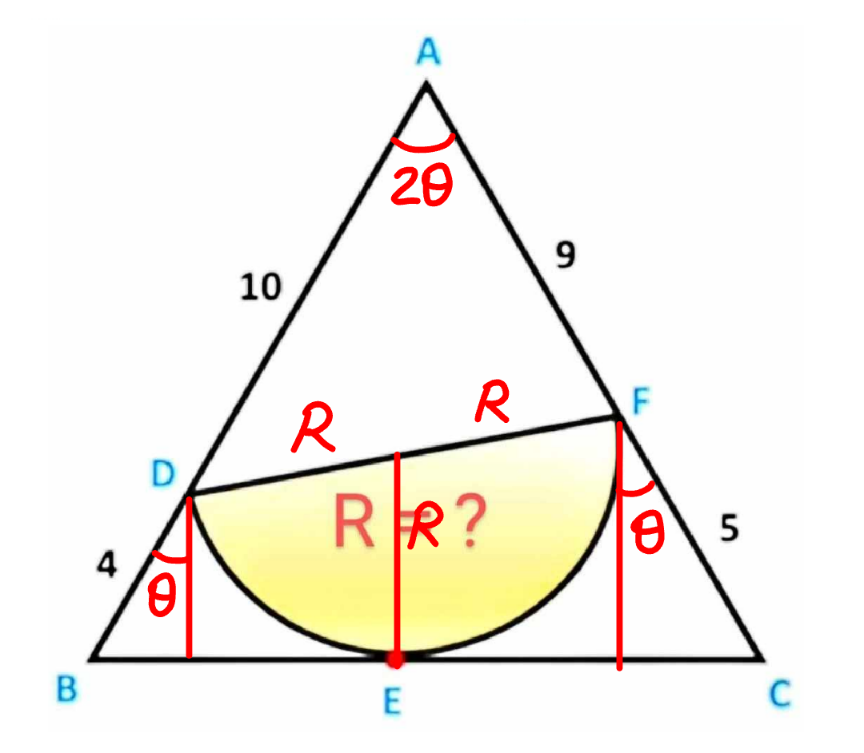
Commented by mr W last updated on 03/May/24
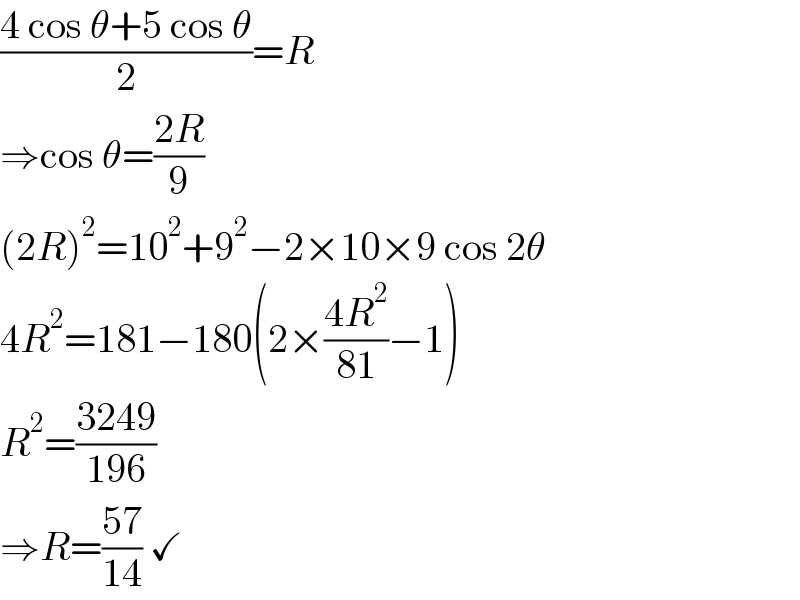
$$\frac{\mathrm{4}\:\mathrm{cos}\:\theta+\mathrm{5}\:\mathrm{cos}\:\theta}{\mathrm{2}}={R} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{2}{R}}{\mathrm{9}} \\ $$$$\left(\mathrm{2}{R}\right)^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}×\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\mathrm{4}{R}^{\mathrm{2}} =\mathrm{181}−\mathrm{180}\left(\mathrm{2}×\frac{\mathrm{4}{R}^{\mathrm{2}} }{\mathrm{81}}−\mathrm{1}\right) \\ $$$${R}^{\mathrm{2}} =\frac{\mathrm{3249}}{\mathrm{196}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{57}}{\mathrm{14}}\:\checkmark \\ $$
Commented by cherokeesay last updated on 03/May/24

$${thank}\:{you}\:{master}\:! \\ $$
