Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 206912 by BaliramKumar last updated on 30/Apr/24

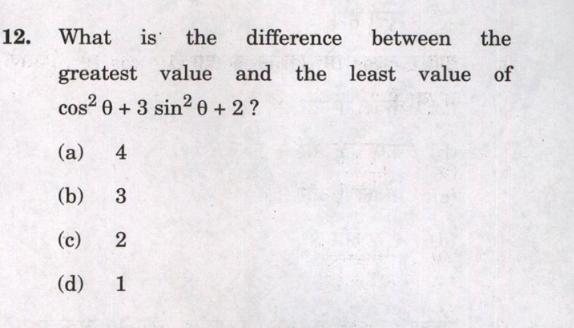
Answered by A5T last updated on 30/Apr/24

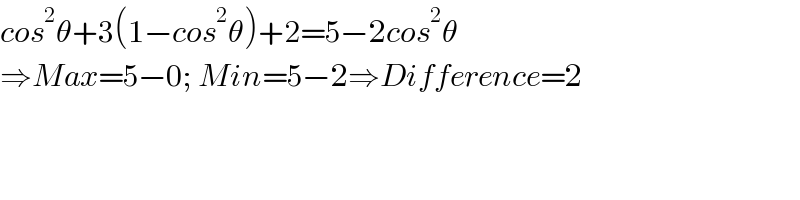
cos^2 θ+3(1−cos^2 θ)+2=5−2cos^2 θ ⇒Max=5−0; Min=5−2⇒Difference=2

$${cos}^{\mathrm{2}} \theta+\mathrm{3}\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)+\mathrm{2}=\mathrm{5}−\mathrm{2}{cos}^{\mathrm{2}} \theta \\ $$$$\Rightarrow{Max}=\mathrm{5}−\mathrm{0};\:{Min}=\mathrm{5}−\mathrm{2}\Rightarrow{Difference}=\mathrm{2} \\ $$

Answered by mr W last updated on 30/Apr/24

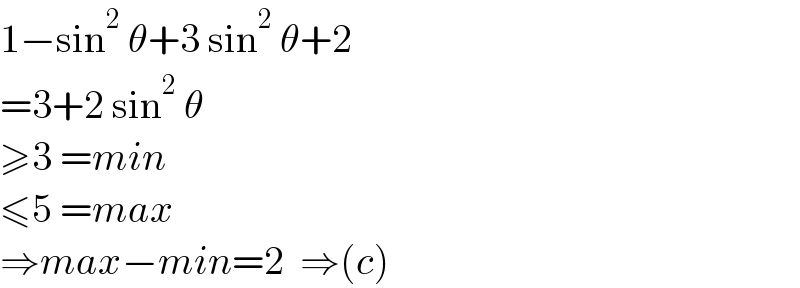
1−sin^2 θ+3 sin^2 θ+2 =3+2 sin^2 θ ≥3 =min ≤5 =max ⇒max−min=2 ⇒(c)

$$\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2} \\ $$$$=\mathrm{3}+\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\geqslant\mathrm{3}\:={min} \\ $$$$\leqslant\mathrm{5}\:={max} \\ $$$$\Rightarrow{max}−{min}=\mathrm{2}\:\:\Rightarrow\left({c}\right) \\ $$

Answered by MM42 last updated on 30/Apr/24

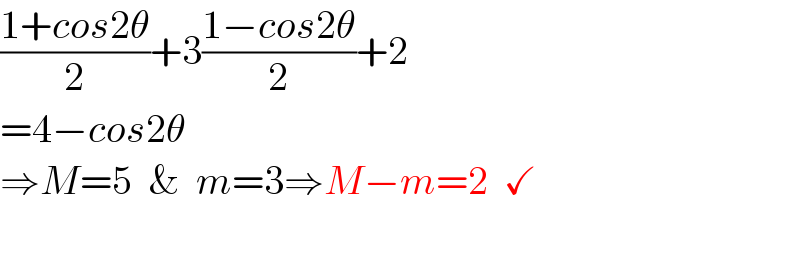
((1+cos2θ)/2)+3((1−cos2θ)/2)+2 =4−cos2θ ⇒M=5 & m=3⇒M−m=2 ✓

$$\frac{\mathrm{1}+{cos}\mathrm{2}\theta}{\mathrm{2}}+\mathrm{3}\frac{\mathrm{1}−{cos}\mathrm{2}\theta}{\mathrm{2}}+\mathrm{2} \\ $$$$=\mathrm{4}−{cos}\mathrm{2}\theta \\ $$$$\Rightarrow{M}=\mathrm{5}\:\:\&\:\:{m}=\mathrm{3}\Rightarrow{M}−{m}=\mathrm{2}\:\:\checkmark \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com