Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 206862 by hardmath last updated on 28/Apr/24

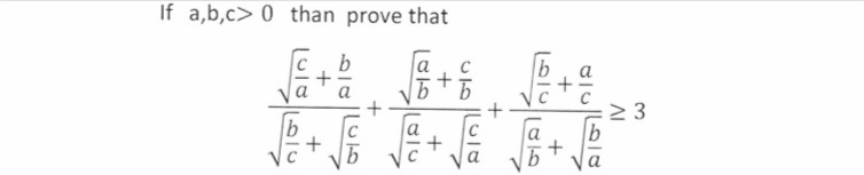
Commented by SWPlaysMC last updated on 29/Apr/24

Easiest way I thought of proving this (I partially solved this) Let a=1, b=1, and c=1 (Hint: if any one of these is 0 then expression is theoretically undefined due to ÷ by 0) (((√(1/1))+(1/1))/( (√(1/1))+(√(1/1))))+(((√(1/1))+(1/1))/( (√(1/1))+(√(1/1))))+(((√(1/1))+(1/1))/( (√(1/1))+(√(1/1))))≥3 so all (√(1/1))=1 and (1/1)=1, thus substitute all nums and denoms with 1+1 like so ((1+1)/(1+1))+((1+1)/(1+1))+((1+1)/(1+1))≥3 1+1=2 and (2/2)=1 so 1+1+1≥3 3≥3 or 3=3 ✓ So a, b, and c all have to be at least ≥1 or the expression will NOT be ≥3 or a≥1, b≥1, c≥1, a+b+c≮3 −−−−−−−−−−−−−−− Work smarter, not harder ;p

$$\mathrm{Easiest}\:\mathrm{way}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{of}\:\mathrm{proving}\:\mathrm{this}\:\left(\mathrm{I}\:\mathrm{partially}\:\mathrm{solved}\:\mathrm{this}\right) \\ $$$$\mathrm{Let}\:{a}=\mathrm{1},\:{b}=\mathrm{1},\:\mathrm{and}\:{c}=\mathrm{1} \\ $$$$\left(\mathrm{Hint}:\:\mathrm{if}\:\mathrm{any}\:\mathrm{one}\:\mathrm{of}\:\mathrm{these}\:\mathrm{is}\:\mathrm{0}\:\mathrm{then}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{theoretically}\:\mathrm{undefined}\:\mathrm{due}\:\mathrm{to}\:\boldsymbol{\div}\:\mathrm{by}\:\mathrm{0}\right) \\ $$$$\frac{\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{1}}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}}+\frac{\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{1}}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}}+\frac{\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{1}}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}}\geqslant\mathrm{3} \\ $$$$\mathrm{so}\:\mathrm{all}\:\sqrt{\frac{\mathrm{1}}{\mathrm{1}}}=\mathrm{1}\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1},\:\mathrm{thus}\:\mathrm{substitute}\:\mathrm{all}\:\mathrm{nums}\:\mathrm{and}\:\mathrm{denoms}\:\mathrm{with}\:\mathrm{1}+\mathrm{1}\:\mathrm{like}\:\mathrm{so} \\ $$$$\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}+\mathrm{1}}+\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}+\mathrm{1}}+\frac{\mathrm{1}+\mathrm{1}}{\mathrm{1}+\mathrm{1}}\geqslant\mathrm{3} \\ $$$$\mathrm{1}+\mathrm{1}=\mathrm{2}\:\mathrm{and}\:\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\:\mathrm{so} \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}\geqslant\mathrm{3} \\ $$$$\mathrm{3}\geqslant\mathrm{3}\:\mathrm{or}\:\mathrm{3}=\mathrm{3}\:\checkmark \\ $$$$\mathrm{So}\:{a},\:{b},\:\mathrm{and}\:{c}\:\mathrm{all}\:\mathrm{have}\:\mathrm{to}\:\mathrm{be}\:\mathrm{at}\:\mathrm{least}\:\geqslant\mathrm{1}\:\mathrm{or}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{will}\:\mathrm{NOT}\:\mathrm{be}\:\geqslant\mathrm{3} \\ $$$$\mathrm{or}\:{a}\geqslant\mathrm{1},\:{b}\geqslant\mathrm{1},\:{c}\geqslant\mathrm{1},\:{a}+{b}+{c}\nless\mathrm{3} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\mathrm{Work}\:\mathrm{smarter},\:\mathrm{not}\:\mathrm{harder}\:;\mathrm{p} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com