
Question Number 206848 by BaliramKumar last updated on 27/Apr/24
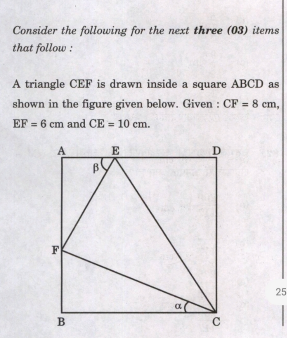
Commented by BaliramKumar last updated on 27/Apr/24

Answered by A5T last updated on 27/Apr/24
![Let side of square=s CE^2 =EF^2 +CF^2 ⇒∠EFC=90°⇒α+β=90° cosα=(s/(CF=8))⇒s=8cosα;BF=8sinα ((sinβ)/(AF=s−8sinα))=(1/(EF=6))⇒s−8sinα=6sinβ ⇒8cosα−8sinα=6cosα⇒8sinα=2cosα ⇒tanα=(1/4)⇒α=tan^(−1) ((1/4)) [ABCD]⇒s^2 =64cos^2 α=64cos^2 (tan^(−1) ((1/4)))=((1024)/(17)) tanα=(1/4);tanβ=((sin(90−α))/(cos(90−α)))=((cosα)/(sinα))=(1/(tanα))=4 ⇒tanα+tanβ=((17)/4) AE=6cosβ=6sinα;DE=s−6sinα =(√((1024)/(17)))−6sin(tan^(−1) ((1/4))) ⇒[CDE]=((DE×DC)/2) =((((√((1024)/(17)))−6sin(tan^(−1) ((1/4))))×(√((1024)/(17))))/2) =((416)/(17))](Q206854.png)
$${Let}\:{side}\:{of}\:{square}={s} \\ $$$${CE}^{\mathrm{2}} ={EF}^{\mathrm{2}} +{CF}^{\mathrm{2}} \Rightarrow\angle{EFC}=\mathrm{90}°\Rightarrow\alpha+\beta=\mathrm{90}° \\ $$$${cos}\alpha=\frac{{s}}{{CF}=\mathrm{8}}\Rightarrow{s}=\mathrm{8}{cos}\alpha;{BF}=\mathrm{8}{sin}\alpha \\ $$$$\frac{{sin}\beta}{{AF}={s}−\mathrm{8}{sin}\alpha}=\frac{\mathrm{1}}{{EF}=\mathrm{6}}\Rightarrow{s}−\mathrm{8}{sin}\alpha=\mathrm{6}{sin}\beta \\ $$$$\Rightarrow\mathrm{8}{cos}\alpha−\mathrm{8}{sin}\alpha=\mathrm{6}{cos}\alpha\Rightarrow\mathrm{8}{sin}\alpha=\mathrm{2}{cos}\alpha \\ $$$$\Rightarrow{tan}\alpha=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\alpha={tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\left[{ABCD}\right]\Rightarrow{s}^{\mathrm{2}} =\mathrm{64}{cos}^{\mathrm{2}} \alpha=\mathrm{64}{cos}^{\mathrm{2}} \left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right)=\frac{\mathrm{1024}}{\mathrm{17}} \\ $$$$ \\ $$$${tan}\alpha=\frac{\mathrm{1}}{\mathrm{4}};{tan}\beta=\frac{{sin}\left(\mathrm{90}−\alpha\right)}{{cos}\left(\mathrm{90}−\alpha\right)}=\frac{{cos}\alpha}{{sin}\alpha}=\frac{\mathrm{1}}{{tan}\alpha}=\mathrm{4} \\ $$$$\Rightarrow{tan}\alpha+{tan}\beta=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$ \\ $$$${AE}=\mathrm{6}{cos}\beta=\mathrm{6}{sin}\alpha;{DE}={s}−\mathrm{6}{sin}\alpha \\ $$$$=\sqrt{\frac{\mathrm{1024}}{\mathrm{17}}}−\mathrm{6}{sin}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right) \\ $$$$\Rightarrow\left[{CDE}\right]=\frac{{DE}×{DC}}{\mathrm{2}} \\ $$$$=\frac{\left(\sqrt{\frac{\mathrm{1024}}{\mathrm{17}}}−\mathrm{6}{sin}\left({tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right)\right)×\sqrt{\frac{\mathrm{1024}}{\mathrm{17}}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{416}}{\mathrm{17}} \\ $$
