Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 206592 by NasaSara last updated on 19/Apr/24

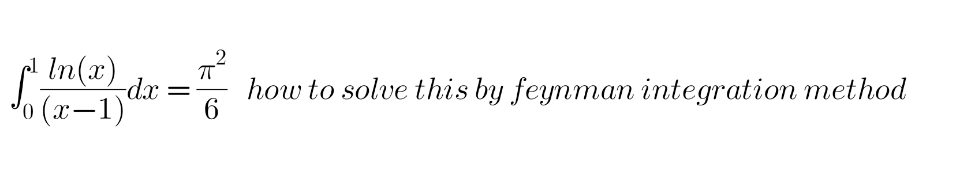
Answered by namphamduc last updated on 20/Apr/24

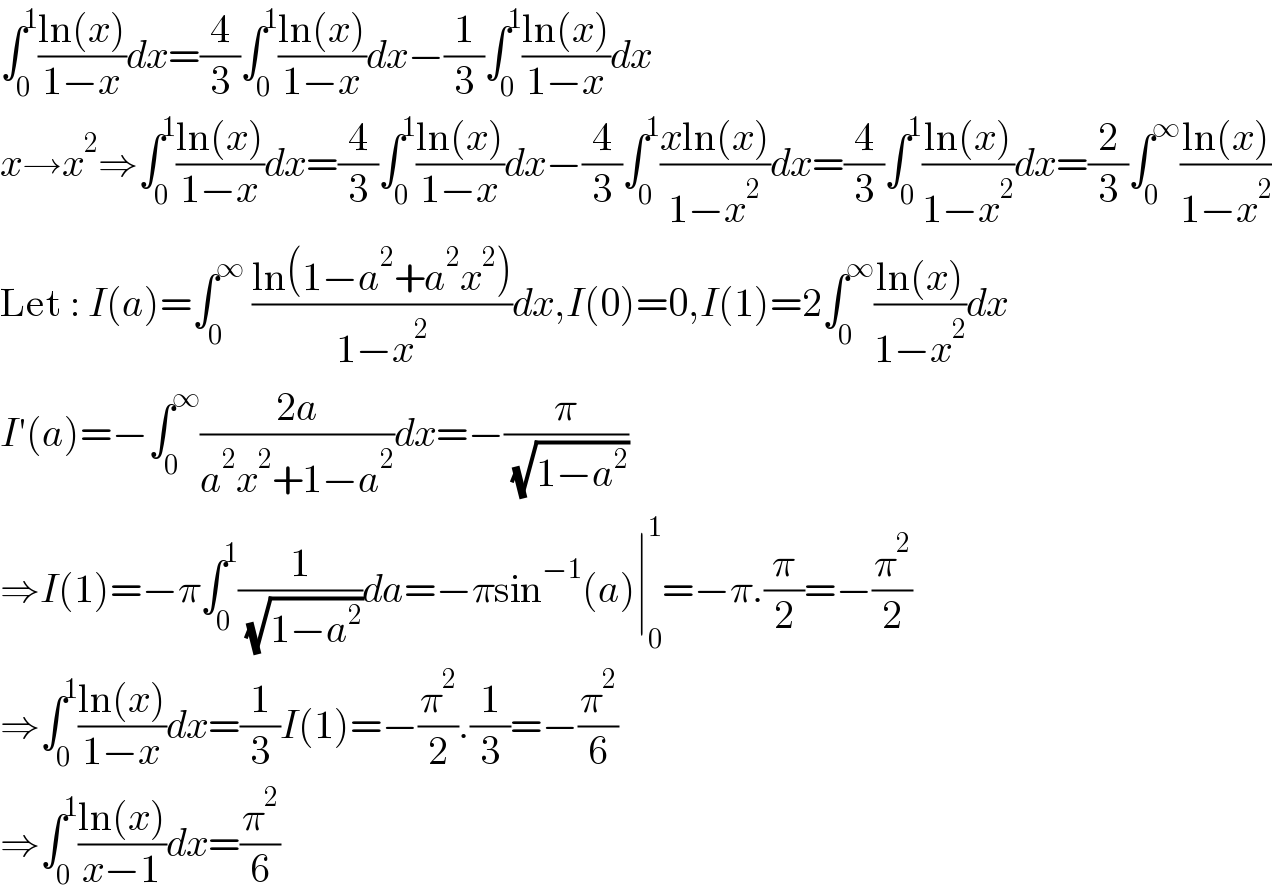
∫_0 ^1 ((ln(x))/(1−x))dx=(4/3)∫_0 ^1 ((ln(x))/(1−x))dx−(1/3)∫_0 ^1 ((ln(x))/(1−x))dx x→x^2 ⇒∫_0 ^1 ((ln(x))/(1−x))dx=(4/3)∫_0 ^1 ((ln(x))/(1−x))dx−(4/3)∫_0 ^1 ((xln(x))/(1−x^2 ))dx=(4/3)∫_0 ^1 ((ln(x))/(1−x^2 ))dx=(2/3)∫_0 ^∞ ((ln(x))/(1−x^2 )) Let : I(a)=∫_0 ^∞ ((ln(1−a^2 +a^2 x^2 ))/(1−x^2 ))dx,I(0)=0,I(1)=2∫_0 ^∞ ((ln(x))/(1−x^2 ))dx I′(a)=−∫_0 ^∞ ((2a)/(a^2 x^2 +1−a^2 ))dx=−(π/( (√(1−a^2 )))) ⇒I(1)=−π∫_0 ^1 (1/( (√(1−a^2 ))))da=−πsin^(−1) (a)∣_0 ^1 =−π.(π/2)=−(π^2 /2) ⇒∫_0 ^1 ((ln(x))/(1−x))dx=(1/3)I(1)=−(π^2 /2).(1/3)=−(π^2 /6) ⇒∫_0 ^1 ((ln(x))/(x−1))dx=(π^2 /6)

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx} \\ $$$${x}\rightarrow{x}^{\mathrm{2}} \Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}−\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{Let}\::\:{I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}−{a}^{\mathrm{2}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx},{I}\left(\mathrm{0}\right)=\mathrm{0},{I}\left(\mathrm{1}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${I}'\left({a}\right)=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{a}}{{a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}−{a}^{\mathrm{2}} }{dx}=−\frac{\pi}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }} \\ $$$$\Rightarrow{I}\left(\mathrm{1}\right)=−\pi\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{da}=−\pi\mathrm{sin}^{−\mathrm{1}} \left({a}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} =−\pi.\frac{\pi}{\mathrm{2}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}=\frac{\mathrm{1}}{\mathrm{3}}{I}\left(\mathrm{1}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{{x}−\mathrm{1}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by NasaSara last updated on 20/Apr/24

thank you

$${thank}\:{you} \\ $$

Answered by Berbere last updated on 20/Apr/24

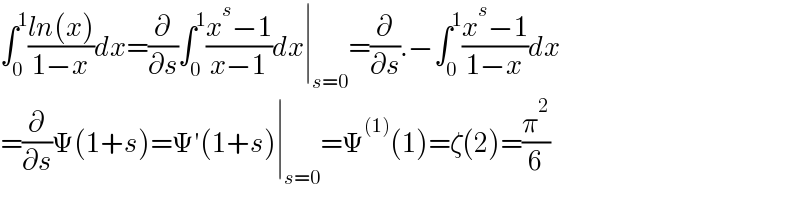
∫_0 ^1 ((ln(x))/(1−x))dx=(∂/∂s)∫_0 ^1 ((x^s −1)/(x−1))dx∣_(s=0) =(∂/∂s).−∫_0 ^1 ((x^s −1)/(1−x))dx =(∂/∂s)Ψ(1+s)=Ψ′(1+s)∣_(s=0) =Ψ^((1)) (1)=ζ(2)=(π^2 /6)

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}−{x}}{dx}=\frac{\partial}{\partial{s}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}} −\mathrm{1}}{{x}−\mathrm{1}}{dx}\mid_{{s}=\mathrm{0}} =\frac{\partial}{\partial{s}}.−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{s}} −\mathrm{1}}{\mathrm{1}−{x}}{dx} \\ $$$$=\frac{\partial}{\partial{s}}\Psi\left(\mathrm{1}+{s}\right)=\Psi'\left(\mathrm{1}+{s}\right)\mid_{{s}=\mathrm{0}} =\Psi^{\left(\mathrm{1}\right)} \left(\mathrm{1}\right)=\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by NasaSara last updated on 20/Apr/24

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com